Shortest Addition Chains

Introduction

A finite sequence of positive integers a0, a1, ..., ar is called an addition chain iff for each element ai, but the first a0 which equals 1, there exist elements in the list with smaller indexes j and k such that ai = aj + ak.
Preciser this is called an addition chain of length r for its last number ar. It can be interpreted like calculating n = ar starting from 1 by addition of only previous calculated numbers. Let us restrict the definition a bit more: addition chains should be strictly monotonic increasing. This can be achived by reordering and dropping multiple numbers. As a consequence a1=2 and a2=3 or 4 always (as long as r > 1). Now ask for the minimal length of an addition chain for a given number n and call this value l(n). If we demand that j or k equals i-1 for all positive indices i -- each ai in the chain requires the previous ai-1, we call such a chain a star-chain and denote its minimal length by l*(n).
I highly recommand Knuth's survey in section 4.6.3 of The Art of Computer Programming, Volume 2: Seminumerical Algorithmus (3. Edition appeared 1997). To illustrate shortest addition chains for each n < 149 one may track the path from the root 1 to the corresponding node n in the following tree:
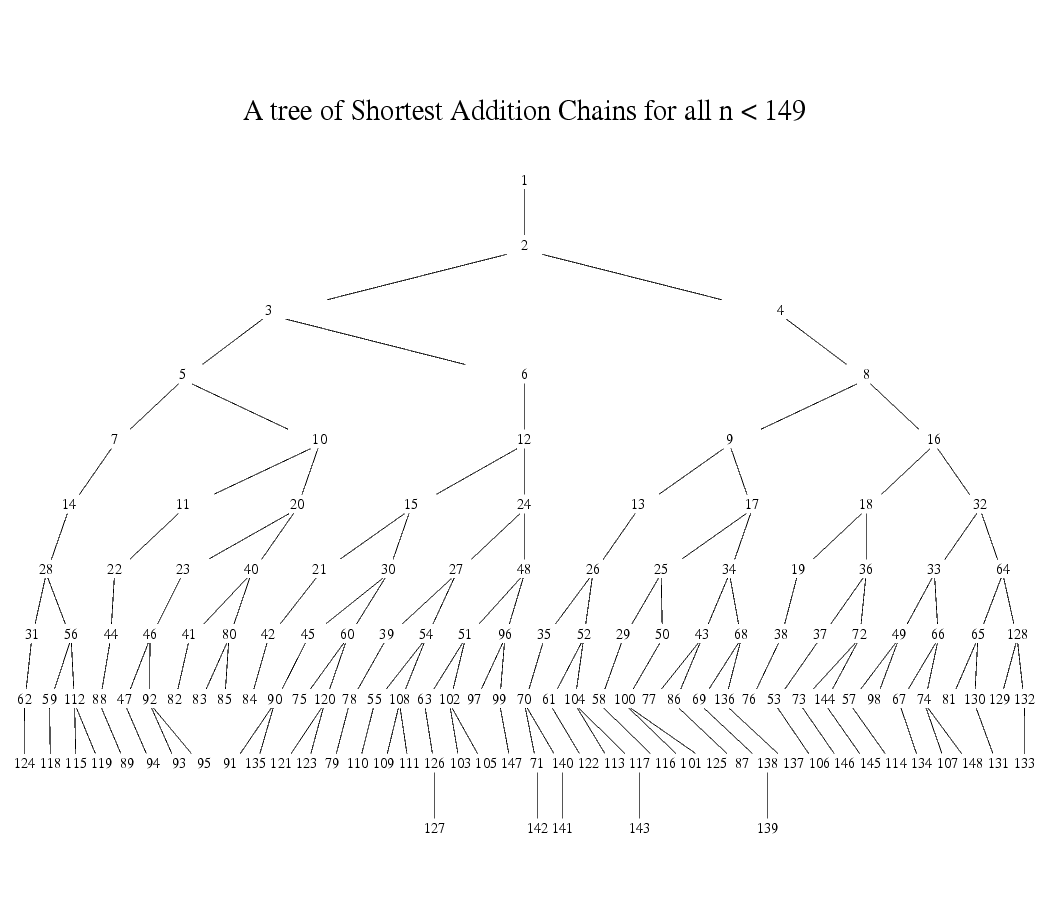
Addition Chain Tree
Such a tree can't be extended gapless to larger n because in the triple 43, 77, 149 any two numbers exclude the third for a shortest addition chain representation in a common tree.

Lower and Upper Bounds of l(n)

Write n in its binary representation and denote by v(n) the number of ones in this representation and by lb(n) the binary logarithm of n rounded to the next integer down in the case it is not already integer (floor-function). Then it is obviously through construction of an addition chain according by the russian multiplication, that l(n) < lb(n) + v(n). An open conjecture states a lower limit of lb(n) + log2(v(n)). Further the difference l(n)-lb(n) is called the number of small steps of n and is denoted by s(n).

Notation

Hint: The definition of v(n), lb(n) and s(n) are in the previous paragraph.
Double step
ai = ai-1 + ai-1
Star step
ai = ai-1 + aj with j < i
Small step
lb(ai) = lb(ai-1)
Standard step
ai = aj + ak with i > j > k

c(r)
the smallest number which has an addition chain of length r
c(r) = min L(r)
m(r)
the median of numbers which have a shortest addition chain of length r
m(r) = med L(r)
μ(r)
the arithemtic average of numbers which have a shortest addition chain of length r
μ(r) = 1/d(r) SUMi e L(r) i
g(r)
the geometric average of numbers which have a shortest addition chain of length r
g(r) = exp( 1/d(r) SUMi e L(r) ln i )
p(r)
the "most probable" number which has a shortest addition chain of length r
p(r) = i: fr(i) = maxh fr(h) with fr(i) = SUM k e N |{ j e L(r): |i-j|=k }|/4k
σ(r)
the standard deviation of the numbers which have a shortest addition chain of length r
σ2(r) = 1/d(r) SUMi e L(r) i2 - μ(r)2
d(r)
the number of numbers which have a shortest addition chain of length r
d(r) = | L(r) |
L(r)
the set of numbers which have a shortest addition chain of length r
L(r) = { i: l(i)=r }

Table of Characterizing Values

r c(r) s(c(r))v(c(r)) μ(r) g(r) m(r)p(r)&sigma(r) d(r) L(r)
0 1 0 1 1.0 1.0 1= 10 1{1}
1 2 0 1 2.0 2.0 2= 20 1{2}
2 3 1 2 3.5 3.5 3+ 3+0.5 2{3,4}
3 5 1 2 6.3 6.2 6= 61.2 3{5,6,8}
4 7 2 3 10.8 10.4 10= 103.1 5{7,9,10,12,16}
5 11 2 3 18.2 17.3 17= 146.1 9{11,13,14,15,17,18,20,24,32}
6 19 2 3 31.7 30.1 28= 2611.4 15{19,21,22,23,25,26,27,28,30,33,34,36,40,48,64}
7 29 3 4 54.5 51.3 49+ 43 21.2 26
8 47 3 5 94.6 88.5 84+ 84 39.0 44
9 71 3 4 162.4 151.0 147+ 116 70.5 78
10 127 4 7 283.1 262.8 248+ 230 125.6 136
11 191 4 7 491.5 456.1 435+ 455 220.8 246
12 379 4 7 869.8 809.4 781+ 840 387.5 432
13 607 4 7 1535.4 1429.4 1372+ 1136 682.3 772
14 1087 4 7 2725.8 2540.0 2461+ 2028 1201.5 1382
15 1903 5 9 4855.4 4527.9 4379= 4047 2122.4 2481
16 3583 5 11 8672.1 8097.2 7813+ 6832 3748.3 4490
17 6271 5 9 15571.7 14570.0 14101+ 12048 6611.3 8170
18 11231 5 11 28094.6 26343.0 25641+ 24096 11694.2 14866
19 18287 5 10 50861.7 47784.4 46466+ 48156 20748.0 27128
20 34303 5 11 92379.2 86937.2 84764+ 89120 36960.6 49544
21 65131 6 12 168192.7 158468.7 154745= 146480 66224.1 90371
22 110591 6 15 306531.6 289025.3 282128+ 290858 119165.8 165432
23 196591 6 16 559476.7 527913.7 514285= 520240 215048.9 303475
24 357887 6 15 1023051.3 966288.1 942710= 1155126 388500.7 558275
25 685951 6 15 1874869.11772876.31732716+ 2310196 702737.4 1028508
26 1176431 6 14 3443135.03259501.83191985+ 2801503 1273563.8 1896704
27 2211837 6 16 6333417.26001516.05881151= 5612462 2313684.8 3501029
28 4169527 7 17 11667084.111064752.410848521+ 9412704 4214352.7 6465774
29 7624319 7 15 21516285.220418193.420044424+ 16905070 7697737.3 11947258
30 14143037 7 16 39714338.937704137.937013874= 41615456 14098404.4 22087489
31 25450463 7 15 73345796.769658962.368327129+ 83230816 25868797.8 40886910
32 46444543 7 18 135563778.8128804664.5126581547+ 132022368 47516034.6 75763102
33 89209343 7 18 250780403.3238406628.4234114742=28495063587306216.3140588339
34 155691199 7 16 434295820+397507456 261070184
35 298695487 7 19 806226456+680509066 485074788
36 550040063 7 17 1497772469+1511488768 901751654
37 994660991 8 18 1677060520
38 1886023151 8 19 3119775195
39 3502562143 8 18
40 6490123999 8 21
41 11889505663 8 21

In the median column the sign = means the value is unique and the character + indicates it lies between the given index and the next index with this r-value because d(r) is even.
With bold font in the previous c(r)-column the sequence of smallest numbers ni is high-lighted which need at least i= s(c(r)) small steps in their addition chain: 1,3,7,29,127,1903,65131,4169527,994660991,....
Moreover here is a graph of c(r) and d(r) together with an approximation function.

Generally Solved Small Step Cases

0-small-step case
Trivial 
  • For each n >= 0 there is exactly 1 0-small-step number in the half-open interval [2^n,2^(n+1)[ .
  • list of all 0-small-step numbers: 
    2^n
  • shortest chains for 0-small-step numbers:
       0(     )  1 
   1( 0, D)  @(A)
1-small-step case
<= 1962 solved
2-small-step case
<= 1973 solved
3-small-step case
1991 solved

History: What was calculated When and by Whom

In July 2004 the data calculated 1997 by Flammenkamp was completely and independently checked. Hereby Neill Clift uncovered four l(n)-errors, which he attributed to a typo in Flammenkamp's program effecting only n-values > 2500000.
On 30th May 2008, Neill Clift discovered the first and smallest n such that l(n) > l(2n).

Data Access

Thanks to Neill Clift's computations you can download the lengths of all shortest additions chains up to n=231 l(n) as bziped2 binary data of 210 MB size. The uncompressed values are coded as l(n)-lb(n)-log2(v(n)) into 2 bits each which the exception of l(2135101487). To decipher this you can download ddt.c compile it and run it with ddt inputfile linelength. You will get all values starting from 1 and broken into lines each containing linelength values onto your stdout from the base-36 alphabet (0,1,2,..,9,a,b,c,..,z) or as a 1 or 2 digit decimal value. A second helper l.c outputs l(n), lb(n), s(n) and v(n) for each given input n which data is in the datafile.
Remark: The smallest n such that l(n)-lb(n)-log2(v(n)) equals 1,2,3,4,... are 29, 3691, 919627, 2135101487, ... .
Look up in the database of the first 231 many l(n) values
starting from index the following values
Table Raw

The effort to compute these values up to n=220 is here visible. The number of cases checked to get l(n) is plotted in red against lb(n) for each number 28 <= n < 220. In blue the number of cases are marked to compute n=c(r) and finally in dark green the average number of cases is drawn which is needed to calculate l(n) for all numbers from 1 up to n (the last gives a good estimate of the average run time of the algorithm).

Generate a Shortest Addition Chain for any given number < 227

n= fast difficult

Conjectures

l(2n-1) <= n + l(n) - 1
The outstanding Scholz-Brauer-Conjecture of 1937. If l(n) is achievable by a star chain then it holds. Therefore only values of n need to be considered with l(n) < l*(n). But the smallest of these numbers is 12509. In August 2005 Neill Clift reported to have confirmed the Scholz-Brauer inequality for all n < 5784689. +
l(2n-1) = n + l(n) - 1
This narrow related equation is proved only for n <= 64  *.
l(n) >= lb(n)+log2(v(n))
This famous lower bound was formulated first a bit differently by Stolarsky 1969 and nearly proved 1974 by Schönhage who showed that l(n) >= log2(n)+log2(v(n))-2.13 holds for each n. In October 2008 Neill Clift confirmed the conjecture for all n <= 264.
log2(c(r)) ~ r - r/log2r
That is the 1997 stated conjecture by Flammenkamp for the asymptotic growth of c(r) outdating the 1991 given assertation that log2(c(r)) ~ r - 2log2r.
Computing l(n) for given n is NP-hard.
Downey, Leony and Sethi didn't prove anything about this statement in their 1981 SIAM article. They proved a similar one, if a set of numbers is given! Many people (and even experts) overlooked this important difference!
+This number 5784689 = 222+97*214+65*24+97 is also the smallest Non-Hansen number (also identified by Neill Clift in 2005 as such).
*In August 2005 Neill Clift reported to have proved equality without any further assumption for all n <= 28 and n = 30. Furthermore in December 2007 he showed equality without any further assumption even for n = 29. Moreover until May 2009 he proved it for all n <= 64

References

legend:
# reviewed journal article
# thesis
# report, memorandum, paper
# conference proceedings
# monography
# unclassified or other

I like to thank Neill Clift, Kirkland, Washington, U.S.A., for far the most references in the preceeding bibliograhy list.

Achim Flammenkamp
Last update: 2011-04-26 13:25:45 UTC+2