Satz des Pythagoras.

Der Satz des Pythagoras erklärt den mathematischen Zusammenhang von den beiden Katheten und der Hypotenuse in einem rechtwinkligen Dreieck. Die Definition beschreibt ihn wie folgt:


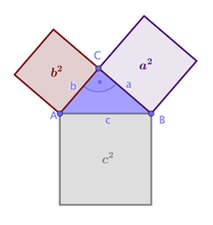
Mit Hilfe der rechten Abbildung, lässt sich dies einfacher erklären: In einem rechtwinkligen Dreieck ist die Fläche a² (Quadrat über der Kathete a) ist zusammen mit der Fläche b² (Quadrat über der Kathete b) genauso groß wie die Fläche c² (Quadrat über der Hypotenuse c).

Packt man diese Definition in eine mathematische Formel, lautet der Satz des Pythagoras:

a² + b² = c²

Die linke Abbildung zeigt dies anhand von Zahlenbeispielen. Du kannst die Punkte A, B und C verschieben.
Mit dieser Formel kann man nun, falls nur zwei Längen von Seiten in einem Dreieck gegeben sind, die dritte Seitenlänge berechnen. Dafür muss man sie nach der gesuchten Seite umstellen. Das Beispiel zeigt die Berechnung von der Seitenlänge a:

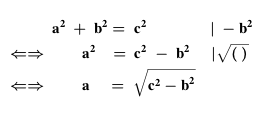
Kannst du die Formel für die anderen Seitenlängen umstellen?

Übrigens, die Umkehrung des Satzes des Pythagoras gilt auch:

Wenn für die Seiten a,b und c eines Dreiecks ABC die Gleichung a² + b² = c² gilt, ist das Dreieck rechtwinklig mit c als Hypotenuse!