A verification system can be viewed as a function which assigns, to a test utterance z and a claimed identity ![]() , a boolean value
, a boolean value ![]() , which is equal to 1 if the utterance is accepted, and 0 if it is rejected.
, which is equal to 1 if the utterance is accepted, and 0 if it is rejected.
Two types of error can then occur. Either a genuine speaker is rejected, or an impostor is accepted. Hence, a false rejection corresponds to:
![]()
and a false acceptance happens if:
![]()
In the rest of this section we will denote the events as follows:
We first address aspects of static evaluation, that is, what meaningful figures can be computed to measure the performance of a system over which the experimentator has absolutely no control. Then, after discussing the role of decision thresholds, we review several approaches that allow a dynamic evaluation of the system to be obtained, i.e. in a relatively threshold-independent manner.
If ![]() , the false rejection rate for speaker
, the false rejection rate for speaker ![]() is defined quite naturally as:
is defined quite naturally as:
![]()
Rate ![]() provides an estimate of
provides an estimate of ![]() , i.e. the probability that the system makes a diagnostic of rejection , given that the applicant speaker is the authorised speaker
, i.e. the probability that the system makes a diagnostic of rejection , given that the applicant speaker is the authorised speaker ![]() (claiming his own identity). If
(claiming his own identity). If ![]() ,
, ![]() is undefined but
is undefined but ![]() .
.
As for closed-set identification , the terms dependable speaker and unreliable speaker can be used to qualify speakers with a low or (respectively) high false rejection rate.
From speaker based figures, the average false rejection rate can be obtained as:
while the gender-balanced false rejection rate is:
where :
The test set false rejection rate is calculated as:
Rates ![]() ,
, ![]() and
and ![]() provide three different estimates of
provide three different estimates of ![]() . Rate
. Rate ![]() is influenced by the test set distribution of genuine attempts which may only be artefactual.
is influenced by the test set distribution of genuine attempts which may only be artefactual.
As opposed to false rejection, there are several ways to score false
acceptance, depending on whether it is the vulnerability of registered
speakers which is considered or the skills of impostors. Moreover, the way to
evaluate false acceptance rates and imposture rates depends on whether the
identity of each impostor is known or not.
KNOWN IMPOSTORS
If the impostor identities are known, the false acceptance rate in
favour of impostor ![]() against registered speaker
against registered speaker ![]() can be defined, for
can be defined, for ![]() , as:
, as:
![]()
Here, ![]() can be viewed as an estimate of
can be viewed as an estimate of ![]() , i.e. the probability that the system makes a diagnostic of acceptance, given that the applicant speaker is the impostor
, i.e. the probability that the system makes a diagnostic of acceptance, given that the applicant speaker is the impostor ![]() claiming identity
claiming identity ![]() .
.
Then, the average false acceptance rate against speaker ![]() can be obtained (if
can be obtained (if ![]() ) by averaging the false acceptances over all impostors:
) by averaging the false acceptances over all impostors:

and similarly the average imposture rate in favour of impostor ![]() can be calculated (for
can be calculated (for ![]() ) as:
) as:
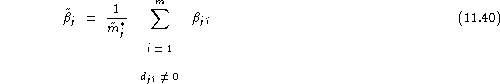
Rates ![]() and
and ![]() provide (respectively)
estimates of
provide (respectively)
estimates of ![]() and
and ![]() under the assumption that all impostors and all claimed
identities are equiprobable. The number
under the assumption that all impostors and all claimed
identities are equiprobable. The number ![]() indicates the
false acceptance rate obtained on average by each
impostor in claiming identity
indicates the
false acceptance rate obtained on average by each
impostor in claiming identity ![]() , while
, while ![]() indicates the
success rate of impostor
indicates the
success rate of impostor ![]() in claiming an identity averaged over each
claimed identity. A registered speaker can be more
or less resistant (low
in claiming an identity averaged over each
claimed identity. A registered speaker can be more
or less resistant (low
![]() ) or vulnerable (high
) or vulnerable (high
![]() ), whereas impostors with a high
), whereas impostors with a high ![]() can be viewed as skilled impostors ,
can be viewed as skilled impostors , as opposed to poor
impostors
as opposed to poor
impostors  for those with a low
for those with a low ![]() .
.
The average false acceptance rate which is equal to the average imposture rate is obtained as:
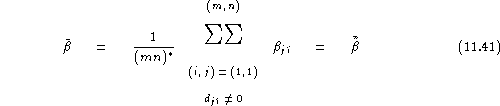
i.e. as the average of the false acceptances over all couples ![]() ,
, which provides an estimate of
which provides an estimate of ![]() under the assumption that all couples
under the assumption that all couples ![]() are equally likely.
are equally likely.
Here, separate estimates of the average false acceptance rate on the male and female registered populations can be obtained as:
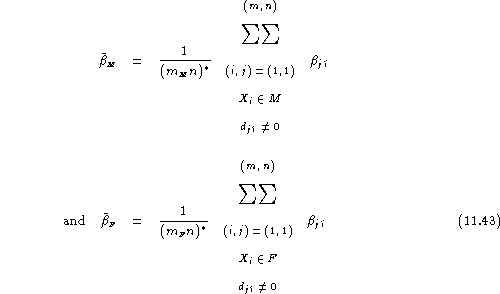
and a gender-balanced false acceptance rate is provided by:
![]()
The question could be raised of whether it is desirable to compute a score which would provide an estimation of the false acceptance rate for a gender-balanced impostor population . We propose not to go that far, as it would clearly lead to duplication of scoring figures, but the influence of impostors' gender could be partly neutralised by the experimental design:
It may also be interesting to calculate imposture rates regardless of the
claimed identities. In this case, we define the imposture rate in favour of impostor ![]() regardless of the claimed identity as:
regardless of the claimed identity as:
![]()
and the average imposture rate regardless of the claimed identity as:

However, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and ![]() cannot be
evaluated when the identities of impostors are not known. In this case false
acceptance rates and imposture rates can be calculated under the assumption
that all impostor test utterances are produced by distinct impostors.
cannot be
evaluated when the identities of impostors are not known. In this case false
acceptance rates and imposture rates can be calculated under the assumption
that all impostor test utterances are produced by distinct impostors.
UNKNOWN IMPOSTORS
The false acceptance rate against speaker ![]() assuming distinct impostors can be obtained (if
assuming distinct impostors can be obtained (if ![]() ) as:
) as:
![]()
and the average false acceptance rate assuming distinct impostors is defined as:

Here again, separate estimates of the average false acceptance rate assuming distinct impostors, on the male and female registered populations can be obtained as:
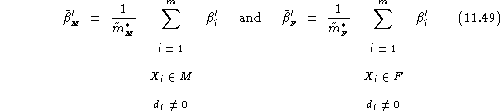
with the gender-balanced false acceptance rate assuming distinct impostors being:
![]()
Rate ![]() provides a speaker-dependent
estimate of
provides a speaker-dependent
estimate of ![]() assuming distinct impostors. Rate
assuming distinct impostors. Rate
![]() can be viewed as an estimate of
can be viewed as an estimate of ![]() under the assumptions of distinct impostors and that all claimed identities
are equally likely while
under the assumptions of distinct impostors and that all claimed identities
are equally likely while ![]() can be
understood as another estimate of
can be
understood as another estimate of ![]() under the
assumptions of distinct impostors, that attempts against male speakers and
against female speakers are equiprobable, and that within a gender class all
claimed identities are equally likely.
under the
assumptions of distinct impostors, that attempts against male speakers and
against female speakers are equiprobable, and that within a gender class all
claimed identities are equally likely.
TEST SET SCORES
If finally false acceptances are scored globally, regardless of the impostor identity nor of the claimed identity, we obtain the test set false acceptance rate which is identical to the test set imposture rate:
![]()
Here, ![]() provides a test set estimate of
provides a test set estimate of ![]() which is biased by the composition of the registered
population and a possible uneveness of the number of impostor trials for each
speaker. Note the relations
which is biased by the composition of the registered
population and a possible uneveness of the number of impostor trials for each
speaker. Note the relations
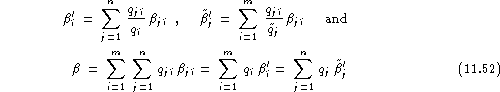
SUMMARY
For scoring false acceptance rates, we believe that, beside ![]() , it is
necessary to report on
, it is
necessary to report on ![]() and
and ![]() (when impostors are known) or
(when impostors are known) or ![]() and
and
![]() (when they are not known), as the score
(when they are not known), as the score
![]() may be significantly influenced by the test data distribution. The
other scores described in this section are mainly useful for diagnostic
analysis.
may be significantly influenced by the test data distribution. The
other scores described in this section are mainly useful for diagnostic
analysis.
It can also be of major interest to estimate the contribution of a given
registered speaker ![]() to the overall false
rejection rate , which can be denoted as
to the overall false
rejection rate , which can be denoted as ![]() , i.e. the probability that the identity of the
speaker was i given that a (false) rejection diagnostic was made on a genuine speaker (claiming his own identity).
, i.e. the probability that the identity of the
speaker was i given that a (false) rejection diagnostic was made on a genuine speaker (claiming his own identity).
We can thus define the average relative unreliability for speaker ![]() as:
as:
![]()
or his test set relative unreliability:
![]()
By construction:
![]()
From a different angle, the relative vulnerability for a given registered
speaker ![]() (i.e.
(i.e. ![]() ) can be measured as his contribution to the false acceptance rate.
) can be measured as his contribution to the false acceptance rate.
Thus, the average relative vulnerability for speaker ![]() can be defined as:
can be defined as:
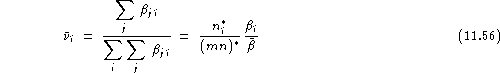
his relative vulnerability assuming distinct impostors, as:
![]()
and his test set relative vulnerability as:
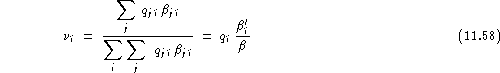
Here:
![]()
Finally, by considering the relative success of impostor ![]() , i.e.
, i.e. ![]() , we define in a dual way, as above, the average imitation ability of impostor
, we define in a dual way, as above, the average imitation ability of impostor ![]() :
:
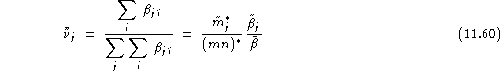
his imitation ability regardless of the claimed identity:
![]()
and his test set relative imitation ability:
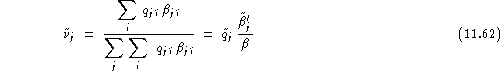
Naturally:
![]()
The relative unreliability and vulnerability can also be calculated relatively to the male/female population.
As for misclassification rates , the gender-balanced, average and test set false rejection rates as well as the gender-balanced and average false acceptance rates assuming distinct impostors and the test set false acceptance rate correspond to different estimates of a global score, under various assumptions on the relative representativity of each genuine test speaker . The discussion of Section 11.4.2 can be readily generalised.
For what concerns gender-balanced and average false
acceptance
rates with known impostors, a relative representativity
![]() can be defined for each couple of registered
speaker and impostor (
can be defined for each couple of registered
speaker and impostor (![]() ) (with
) (with
![]() ), and if we write:
), and if we write:
![]()
we have:
![]()
for ![]()
![]()
for ![]()
In the case of casual impostors , choosing a selective attempt configuration towards same-sex speakers is equivalent to the assumption:
![]()
i.e. that the representativity of a cross-sex attempt is zero.
Studies allowing better definition of the representativity of impostor attempts against registered speakers would be of great help to increase the relevance of evaluation scores.
Tables 11.4, 11.5 and 11.6 give examples of false acceptance rates , false rejection rates , and imposture rates, as well as unreliability, vulnerability and imitation ability. As for the closed-set identification examples, the number of tests used to design these examples is too small to guarantee any statistical validity.
Out of 18 genuine attempts, 6 false rejections are observed, hence the test set false acceptance rate. Nevertheless, the 3 false rejections out of 9 trials for
do not have the same impact on the average false rejection rate
as the 3 false rejections out of 7 trials for
. In fact, while
seems to be the most reliable speaker,
appears more unreliable than
on the average, as, for what concerns relative unreliability scores,
.
| m=3 | ||||||
| | | | ||||
| Against Male | Against Female | |||||
| n = 2 | n = 2 | n = 2 | ||||
| | | | | | | |
| | | | | - | | |
| 4 | 2 | 1 | 2 | - | 4 | |
| 6 | 2 | 6 | 3 | - | 5 | |
| 8 | 9 | 5 | ||||
| d | 22 | |||||
| 2 | 2 | 1 | ||||
| 3 | ||||||
| 5 | ||||||
| | 0 | | | undef. | | |
| | | | ||||
| | ||||||
| | | | ||||
| | ||||||
| | ||||||
| 2 | 1 | |||||
| 4 | 1 | |||||
| | | |||||
| | ||||||
| | | |||||
| | ||||||
| | | | ||||
| | | | ||||
| | | | ||||
n=2 ![]()
![]()
m = 3 m = 3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- ![]()
![]()
![]()
![]()
4 1 - 2 2 4 ![]()
6 6 - 2 3 5 ![]()
12 10 d 22 ![]()
2 3 ![]()
2 ![]()
5 ![]()
![]()
![]()
undef. 0 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out of 6 trials from impostoragainst speaker
, 2 of them turned out to be successful, while out of 6 other trials against
, 5 lead to a (false) acceptance . As no attempts from
against
were recorded, the average imposture rate from impostor
can be estimated as
. If we now ignore the actual identities of violated speakers , and we summarise globally the success of impostor
, we get
which turns out to be also equal to
. While
and
, the average imposture rate regardless of the claimed identity
indicates that the ``average'' impostor is successful almost 2 times out of 5 in his attempts. All estimates of the relative imitation ability (
,
and
) agree that
is a much more skilled impostor than
who seems to be quite poor.
From now on, we will denote as ![]() and
and ![]() the false rejection and acceptance rates, whichever exact estimate is really chosen.
the false rejection and acceptance rates, whichever exact estimate is really chosen.
Estimates of the following quantities are required:
With the estimates the expected benefit ![]() of a verification system with false rejection rate
of a verification system with false rejection rate ![]() and false acceptance rate
and false acceptance rate ![]() can be computed as:
can be computed as:
In particular, when ![]() and
and ![]() , the equal-risk equal-cost expected benefit is:
, the equal-risk equal-cost expected benefit is:
![]()
The expected benefit is usually a meaningful static evaluation figure for the potential clients of the technology. It must however be understood only as the average expected benefit for each user attempt. It does not take into account external factors such as the psychological impact of the system, its maintenance costs, etc.
Speaker verification systems usually
proceed in two steps. First, a matching score ![]() is
computed between the test utterance z and the
reference model
is
computed between the test utterance z and the
reference model ![]() corresponding to the claimed identity. Then,
the value of the matching score is compared to a threshold
corresponding to the claimed identity. Then,
the value of the matching score is compared to a threshold
![]() , and a decision is taken as follows:
, and a decision is taken as follows:
![]()
In other words, verification is positive only if the match between the test utterance and the reference model (for the claimed identity) is close enough.
A distinction can be made depending on whether each registered
speaker has his individual threshold or whether a
single threshold is used which is common to all speakers. In other words, if
![]() depends on i, the system uses speaker-dependent
thresholds , whereas if
depends on i, the system uses speaker-dependent
thresholds , whereas if ![]() does not depend on i, the system uses
a speaker-independent threshold.
does not depend on i, the system uses
a speaker-independent threshold.
 We will
denote as
We will
denote as ![]() the threshold vector
the threshold vector ![]() , and
as
, and
as ![]() and
and ![]() the false rejection
and acceptance rates corresponding to
the false rejection
and acceptance rates corresponding to
![]() .
.
The values of ![]() have an inverse impact on the false
rejection rate and on the false acceptance
rate . Thus, with a low
have an inverse impact on the false
rejection rate and on the false acceptance
rate . Thus, with a low ![]() , fewer genuine
attempts from speaker
, fewer genuine
attempts from speaker ![]() will be rejected, but more impostors will be
erroneously accepted as
will be rejected, but more impostors will be
erroneously accepted as ![]() . Conversely, if
. Conversely, if ![]() is increased,
is increased,
![]() will generally decrease, at the expense of an increasing
will generally decrease, at the expense of an increasing
![]() . The goal of dynamic evaluation is to provide a description
of the system performance which is as independent as possible of the threshold
values.
. The goal of dynamic evaluation is to provide a description
of the system performance which is as independent as possible of the threshold
values.
The setting of thresholds is conditioned to the specification of an operating constraint which expresses the compromise that has to be reached between the two types of error. Among many possibilities, the most popular ones are:
| if | | then | |
| if | | then | |
In most practical applications, however, the equal error rate does not correspond to an interesting operating constraint.
Two procedures are classically used to set the thresholds: the a priori threshold setting procedure and the a posteriori threshold setting procedure.
When the a priori threshold setting procedure is implemented, the
threshold vector ![]() is estimated from a set of
tuning data, which can be either the training data themselves, or a new set
of unseen data. Then, the false rejection and acceptance rates
is estimated from a set of
tuning data, which can be either the training data themselves, or a new set
of unseen data. Then, the false rejection and acceptance rates
![]() and
and ![]() are estimated on a
disjoint test set . Naturally, there must be no intersection between the tuning
data set and the test data set. Not only must the speech material of genuine
attempts and impostor attempts be different between these two sets, but also
the bundle of pseudo-impostors used to tune the
threshold for a registered speaker should not contain any of the impostors
which will be tested against this very speaker within the test set. Of course,
the volume of additional speech data used for threshold setting must be
counted as training material , when reporting on the training speech
quantity.
are estimated on a
disjoint test set . Naturally, there must be no intersection between the tuning
data set and the test data set. Not only must the speech material of genuine
attempts and impostor attempts be different between these two sets, but also
the bundle of pseudo-impostors used to tune the
threshold for a registered speaker should not contain any of the impostors
which will be tested against this very speaker within the test set. Of course,
the volume of additional speech data used for threshold setting must be
counted as training material , when reporting on the training speech
quantity.
When the a posteriori threshold setting procedure is adopted, ![]() is set on the test data themselves. In this case,
the false
rejection and acceptance rates
is set on the test data themselves. In this case,
the false
rejection and acceptance rates ![]() and
and
![]() must be understood as the performance of the system
with ideal thresholds. Though this procedure does not lead to a fair
measure of the system performance, it can be interesting, for diagnostic
evaluation , to compare
must be understood as the performance of the system
with ideal thresholds. Though this procedure does not lead to a fair
measure of the system performance, it can be interesting, for diagnostic
evaluation , to compare ![]() and
and ![]() with
with ![]() and
and ![]() .
.
Whichever operating constraint is chosen to tune the thresholds is only one of the infinite number of possible trade-offs, and it is generally not possible to predict, from the false rejection and false acceptance rates obtained for a particular functioning point, what would be the error rates for another functioning point. In order to be able to estimate the performance of the system under any conditions, its behaviour has to be modelled so that its performance can be characterised independently from any threshold settings.
SPEAKER-INDEPENDENT THRESHOLD
In the case of a speaker-independent threshold, the false
rejection and the false acceptance rates
can be written as functions of a single parameter ![]() ,
namely
,
namely ![]() and
and ![]() . Then, a more
compact way of summarising the system's behaviour consists in expressing
. Then, a more
compact way of summarising the system's behaviour consists in expressing
![]() directly as a function of
directly as a function of ![]() (or the opposite), that is:
(or the opposite), that is:
![]()
Using terminology derived from Communication Theory, function f is
sometimes called the Receiver Operating Characteristic
and the corresponding curve ![]() the ROC curve. Generally, function f is monotonically decreasing and satisfies the limit conditions
the ROC curve. Generally, function f is monotonically decreasing and satisfies the limit conditions ![]() and
and ![]() . Figure 11.1 depicts a typical ROC curve.
. Figure 11.1 depicts a typical ROC curve.
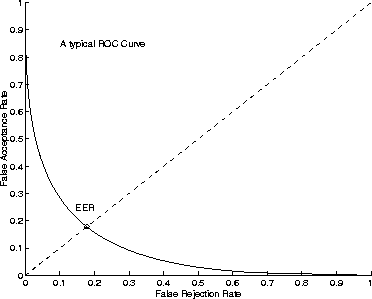
Figure 11.1: A typical ROC curve and its equal error rate
The point-by-point knowledge of function f provides a threshold-independent description of all possible functioning conditions of the system. In particular:
In practice, there are several ROC curves, depending on what type of false rejection and acceptance scores are used:
SPEAKER-DEPENDENT THRESHOLDS
In the case of speaker-dependent thresholds, the false rejection and the false acceptance rates for each speaker ![]() depend on a different parameter
depend on a different parameter ![]() . Therefore, each speaker has his own ROC curve:
. Therefore, each speaker has his own ROC curve:
![]()
In this case, there is no simple way of deriving an ``average'' ROC curve that would represent the general behaviour of the system. Current practice consists in characterising each individual ROC curve by its equal error rate ![]() , and in summarising the performance of the system by the average equal error rate
, and in summarising the performance of the system by the average equal error rate ![]() computed as:
computed as:
![]()
Note here that a gender-balanced equal error
rate
![]() can be defined as:
can be defined as:
![]()
and a test set equal error rate as:
![]()
Though we used the same terminology for denominating equal error rates with speaker-dependent and speaker-independent thresholds , it must be stressed that the scores are not comparable. Therefore it should always be specified in which framework they are computed.
Equal error rates can be interpreted as a very
local property of the ROC
curve. In fact, as the ROC
curve usually has its concavity turned in the direction of the axis ![]() , the EER gives an idea of how close the ROC curve is to the axes. However, this is a very incomplete picture of the general system performance level, as it is virtually impossible to predict the performance of the system under a significantly different operating condition.
, the EER gives an idea of how close the ROC curve is to the axes. However, this is a very incomplete picture of the general system performance level, as it is virtually impossible to predict the performance of the system under a significantly different operating condition.
Recent work by [Oglesby (1994)] has addressed the question of how to encapsulate the entire system characteristic into a single number. Oglesby's suggestions, which we will develop now, consist in finding a simple 1-parameter model which describes as accurately as possible the ROC curve over most of its definition domain. If the approximation is good enough, reasonable error rate estimates for any functioning point can be derived. As in the last section, we will first discuss the case of a system with a speaker-independent threshold, and then extend the approach to speaker-dependent thresholds.
For modelling the relation between ![]() and
and ![]() , the simplest approach is to assume a linear operating characteristic, i.e. a relation between
, the simplest approach is to assume a linear operating characteristic, i.e. a relation between ![]() and
and ![]() of the kind:
of the kind:
![]()
where ![]() is a constant which can be understood as the
linear-model EER.
is a constant which can be understood as the
linear-model EER.  However, typical ROC
curves do not have a linear
shape at all, and this model is too poor
to be effective over a large domain.
However, typical ROC
curves do not have a linear
shape at all, and this model is too poor
to be effective over a large domain.
A second possibility is to assume that the ROC curve has the approximate shape of the positive branch of a hyperbola, which supposes the relation:
![]()
Here ![]() is another constant which can be interpreted as
the hyperbolic-model EER. The hyperbolic model is equivalent to a
linear model in the log-error domain. It usually fits the
ROC
curve much better.
is another constant which can be interpreted as
the hyperbolic-model EER. The hyperbolic model is equivalent to a
linear model in the log-error domain. It usually fits the
ROC
curve much better. However, it has the drawback of not fulfilling the limit conditions, as
However, it has the drawback of not fulfilling the limit conditions, as ![]() and
and ![]() .
.
A third possibility, proposed by Oglesby , is to use the following model:
where ![]() will be referred to as Oglesby's model EER
. Oglesby reports a good fit of the model with experimental data, and underlines the fact that
will be referred to as Oglesby's model EER
. Oglesby reports a good fit of the model with experimental data, and underlines the fact that ![]() and
and ![]() .
.
The parametric approach is certainly a very relevant way to give a broader system characterisation. Nevertheless, several issues remain questionable.
First, it is clear that none of the models proposed above account for a possible skewness of the ROC curve. As Oglesby notes it, to address skewed characteristics would require introducing an additional variable, which would give rise to a second, non-intuitive, figure.
A second question is what criterion ![]() should be minimised to fit the model curve
should be minimised to fit the model curve ![]() to the true ROC curve
to the true ROC curve ![]() . If we denote as
. If we denote as ![]() the optimisation domain on which the best fit is to be found, the most natural criterion would be to minimise the mean square error between
the optimisation domain on which the best fit is to be found, the most natural criterion would be to minimise the mean square error between ![]() and
and ![]() over the interval
over the interval ![]() . However, an absolute error difference does not have the same meaning when
. However, an absolute error difference does not have the same meaning when ![]() changes order of magnitude, and an alternative could be to minimise the mean square error between the curves in a log-log representation.
changes order of magnitude, and an alternative could be to minimise the mean square error between the curves in a log-log representation.
A third and most crucial question is how the unavoidable deviations between the model and the actual ROC curve should be quantified and reported.
Here is a possible answer to these questions. Though the approach that we are going to present has not been extensively tested so far, we believe that it is worth exploring it in the near future, as it may prove useful to summarise concisely the performance of a speaker verification system, in a relatively meaningful and exploitable manner.
The solution proposed starts by fixing an accuracy ![]() for the ROC curve modelling, say for instance
for the ROC curve modelling, say for instance ![]() . Then, if we define:
. Then, if we define:
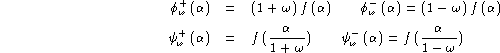
the following properties are obvious:
Hence, when both constraints are satisfied, both relative differences between the modelled and exact false rejection and acceptance rates are below ![]() .
.
Then, a model of the ROC curve must be chosen, for instance Oglesby's model . However, if another model fits the curve better, it can alternatively be used, but it preferably should depend on a single parameter, and the link between the value of this parameter and the model equal error rate should be specified.
For a given parameter ![]() , the lower and upper bound of the
, the lower and upper bound of the ![]() -accuracy false rejection rate validity domain,
-accuracy false rejection rate validity domain, ![]() and
and ![]() are obtained by decreasing (or increasing)
are obtained by decreasing (or increasing) ![]() , starting from the initial value
, starting from the initial value ![]() , until one of the two constraints of equations (11.78) and (11.80) is no more satisfied. This process can be repeated for several values of
, until one of the two constraints of equations (11.78) and (11.80) is no more satisfied. This process can be repeated for several values of ![]() varying for instance in small steps within the interval
varying for instance in small steps within the interval ![]() . Finally, the value of
. Finally, the value of ![]() corresponding to the wider validity domain can be chosen as the system performance measure, in the validity domain of the approximation. Note that
corresponding to the wider validity domain can be chosen as the system performance measure, in the validity domain of the approximation. Note that ![]() does not need to be inside the validity domain for its value to be meaningful.
does not need to be inside the validity domain for its value to be meaningful.
If the validity domain turns out to be too small, then the process could be
repeated after having set the accuracy ![]() to a higher
value. Another possibility could be to give several model equal error
rates , corresponding to several adjacent
validity domains (with a same accuracy
to a higher
value. Another possibility could be to give several model equal error
rates , corresponding to several adjacent
validity domains (with a same accuracy ![]() ), i.e. a
piecewise representation of the ROC curve.
), i.e. a
piecewise representation of the ROC curve.
A first advantage of the parametric description is that it allows prediction
of the behaviour of a speaker verification system
for a more or less extended set of operating conditions. It could then be
possible to give clear answers to a potential client of the technology, as
long as this client is able to specify his constraints. The second advantage
is that the model EER is a number which
relates well to the conventional EER . Therefore the new description would not require that the scientific
community totally changes its point of view in apprehending the performance
of a speaker verification system. The
main drawback of the proposed approach is that it lacks experimental
validation for the time being. Therefore, we suggest adopting it as an
experimental evaluation methodology, until it has been proven efficient.
The
main drawback of the proposed approach is that it lacks experimental
validation for the time being. Therefore, we suggest adopting it as an
experimental evaluation methodology, until it has been proven efficient.
In dealing with a system using speaker-dependent thresholds , we are brought back to the difficulty of averaging ROC curve models across speakers.
The ROC curve for each speaker ![]() can be summarised by a model equal error rate
can be summarised by a model equal error rate ![]() and a
and a ![]() -accuracy false acceptance rate validity domain
-accuracy false acceptance rate validity domain ![]() .
Lacking a more relevant solution, we suggest characterising the average system performance by averaging across speakers the model EER , and the bounds of the validity interval.
Thus the global system performance could be given as an average model EER :
.
Lacking a more relevant solution, we suggest characterising the average system performance by averaging across speakers the model EER , and the bounds of the validity interval.
Thus the global system performance could be given as an average model EER :
![]()
and an average ![]() -accuracy false acceptance rate validity domain:
-accuracy false acceptance rate validity domain:
![]()
where:
![]()
The same approach can be implemented, with different weights, to compute a
gender-balanced model EER
![]() and a
test set model EER
and a
test set model EER ![]() , and the
corresponding validity domains.
, and the
corresponding validity domains.
Another possibility would be to fix a speaker-independent
validity domain
![]() for each ROC
curve, and then compute the individual accuracy
for each ROC
curve, and then compute the individual accuracy
![]() . Then, to obtain a global
. Then, to obtain a global score,
all
score,
all ![]() could be averaged (using weights depending on the type of
estimate), and the performance would be a global model equal error
rate together with a false
acceptance rate domain
could be averaged (using weights depending on the type of
estimate), and the performance would be a global model equal error
rate together with a false
acceptance rate domain ![]() common to all speakers, but at an average accuracy.
common to all speakers, but at an average accuracy.
For example, consider a verification system with a speaker-independent
threshold that has a gender-balanced Oglesby's equal error
rate
of ![]() with a
with a ![]() -accuracy false
rejection rate validity domain of
-accuracy false
rejection rate validity domain of ![]() . Here, the
ROC curve under consideration
is
. Here, the
ROC curve under consideration
is ![]() . We will denote now
. We will denote now
![]() and
and
![]() , for simplicity reasons.
, for simplicity reasons.
For any false rejection rate a satisfying ![]() , the difference between the actual false acceptance
rate b and the estimated false acceptance
rate
, the difference between the actual false acceptance
rate b and the estimated false acceptance
rate ![]() predicted by Oglesby's model
with parameter
predicted by Oglesby's model
with parameter
![]() satisfies
satisfies
![]() . It can then be computed (using
equation (11.77)) that the
. It can then be computed (using
equation (11.77)) that the ![]() -accuracy false
acceptance
rate validity domain is
-accuracy false
acceptance
rate validity domain is ![]() , and it is guaranteed that, for
any value of b in this interval, the difference between the actual false
rejection rate a and the estimated false
rejection rate
, and it is guaranteed that, for
any value of b in this interval, the difference between the actual false
rejection rate a and the estimated false
rejection rate ![]() (predicted by
Oglesby's model with EER 0.047) satisfies
(predicted by
Oglesby's model with EER 0.047) satisfies
![]() . In particular, the exact
(gender-balanced) EER of the system,
. In particular, the exact
(gender-balanced) EER of the system, ![]() , is equal to 0.047, at a
, is equal to 0.047, at a ![]() relative accuracy.
relative accuracy.