A closed-set identification system can be viewed as a function which
assigns, to any test utterance z, an estimated speaker index
, corresponding to the identified speaker
in the set of registered speakers .
In closed-set identification, all test utterances belong to one of the
registered speakers . Therefore, a misclassification error occurs
for test utterance number k produced by speaker 
when:
where 
denotes the Kronecker function, which is 1 if the
two arguments are the same and 0 otherwise.
The most natural figure that indicates the performance of a speaker identification system is the relative number of times the system fails in correctly identifying an applicant speaker ; in other words, how often a test utterance will be assigned an erroneous identity. Whereas it is straightforward to calculate a performance figure on a speaker-by-speaker basis, care should be taken when deriving a global score.
With our notation, and assuming that 
, we define the
misclassification rate for speaker as:
If we denote as 
the
probability that the system under test identifies another speaker
(with index j) than the actual speaker , the quantity
provides an estimate of this probability, whereas
provides an estimate of 
. However, it is preferable to report error
scores rather than success scores, and performance improvements should
be measured as relative error rate reduction.
If 
, is undefined but
.
We suggest using the term dependable speaker to qualify a
registered speaker with a low misclassification rate , and the term
unreliable speaker for a speaker with a high misclassification
rate .
From speaker-by-speaker figures, the average misclassification rate can be derived as:
and by computing separately:
the gender-balanced misclassification rate can be obtained as:
The previous scores are different from the test set misclassification rate , calculated as:
Scores 
and 
are formally identical if and only if
does not depend on i, i.e. when the test set contains an identical
number 
test utterances for each speaker. As it is usually
observed that speaker recognition performances may vary with the speaker's
gender, the comparison of and 
can show significant differences, if the registered population is not
gender-balanced . Therefore, we believe that an accurate description of the
identification performance requires the three numbers
, , and to be
provided.
Taking another point of view, performance scores can be designed to
measure how reliable the decision of the system is when it has
assigned a given identity; in other words, to provide an estimate of
the probability 
, i.e. the
probability that the speaker is not really when the
system under test has output as the most likely identity.
To define the mistrust rate, we have to introduce the following notation:
By definition, 
and 
are respectively the number and
proportion of test utterances identified as over the whole test set ,
while 
is the number of registered speakers whose identity was
assigned at least once to a test utterance.
The mistrust rate for speaker can then be computed (for 
) as:
Here again, if 
, 
is undefined, but 
.
We suggest that the term resistant speaker could be used to
qualify a registered speaker with a low mistrust rate, and the term vulnerable speaker for a
speaker with a high mistrust rate.
From this speaker-by-speaker score, the average mistrust rate can be derived as:
the gender-balanced mistrust rate is defined as:
By noticing now that:
there appears to be no need to define a test set mistrust rate
. In other words: the test set mistrust rate is equal to
the test set misclassification rate.
From a practical point of view, misclassification rates and mistrust rates can be obtained by the exact same scoring programs, operating successively on the confusion matrix and on its transpose.
Most speaker identification systems use a similarity measure between a test utterance and all training patterns to decide, by a nearest neighbour decision rule, which is the identity of the test speaker. In this case, for a test utterance x, an ordered list of registered speakers can be produced:
where, for all index j, 
is judged closer to the test
utterance than 
is.
The identification rank of the genuine speaker of utterance
can then be expressed as:
In other words, 
is the position at which the correct speaker appears in
the ordered list of neighbours of the test utterance . Note that a correct
identification of corresponds to 
.
Under the assumption that , let us now denote:
The 
confidence rank for speaker , which we
will denote here as 
can then be defined
as the smallest integer number for which of the test
utterances belonging to speaker are part of the 
nearest neighbours in the ordered list of candidates. Hence the
formulation:
Then, the average confidence rank can be computed as the average of over all registered speakers (for which ):
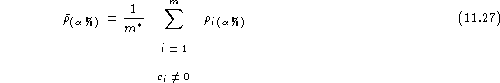
Though a gender-balanced confidence rank could be defined analogously to gender-balanced misclassification and mistrust rates, the relevance of this figure is not clear.
If finally we denote:
the test set confidence rank is defined as:
Average scores, gender-balanced scores and
test set scores all fall under the
same formalism. If we denote as 
a certain quantity which we will
call the relative representativity of speaker and which
satisfies 
, and if we now consider the linear combination:
It is clear that:
 | for  |
 | for  |
 | for  |
Therefore , and
correspond to different estimates of a global score, under various assumptions
on the relative representativity of each speaker. For average scores,
it is assumed that each speaker is equally representative, irrespectively of
its sex group, but if the test population is strongly unbalanced this
hypothesis may not be relevant (unless there is a reason for it). For
gender-balanced scores , each test speaker is supposed to be representative of
its sex group, and each sex group is supposed to be
equiprobable. Test set
scores make the assumption that each test speaker has a representativity which
is proportional to its number of test utterances , which is certainly not
always a meaningful hypothesis.
Test set scores can therefore be used as an overall performance measure if the test data represent accurately the profile and behaviour of the user population, both in terms of population composition and individual frequency of use. If only the composition of the test set population is representative of the general user population, average scores allow neutralisation of the possible discrepancies in number of utterances per speaker. If finally the composition of the test set speaker population is not representative, gender-balanced scores provide a general purpose estimate.
If there is a way to estimate separately the relative representativity for each test registered speaker , a representative mi sclassification rate can be computed as in equation (11.30). Conversely, some techniques such as those used in public opinion polls can be resorted to in order to select a representative test population when setting up an evaluation experiment.
