Many applications in language engineering require testing of hypotheses. An example from the scenario given in Section 9.1.2 was testing whether there were differences between read and spontaneous speech with respect to selected statistics. If the statistic was mean vowel duration in the two conditions where speech was recorded, we have a situation calling for simple hypothesis testing. This situation is called simple hypothesis testing since it involves a parameter of a single population.
Following the approach adopted so far, the concepts involved
in such testing will be illustrated for this selected example. The
first step is to make alternative assertions about what the likely
outcome of an analysis might be. One assertion is that the analysis
might provide no evidence of a difference between the two
conditions. This case is referred to as the null hypothesis
(conventionally abbreviated as H![]() ) and
asserts here that the mean tone unit duration
in the read speech is the same
as that in the spontaneous speech .
) and
asserts here that the mean tone unit duration
in the read speech is the same
as that in the spontaneous speech .
Other assertions might be made about this situation. These are referred to as alternative hypotheses. One alternative hypothesis would be that the tone unit duration of the read speech will be less than that of the spontaneous speech . A second would be the converse, i.e. the tone unit duration of the spontaneous speech will be less than that of the read speech . The decision about which of these alternate hypotheses to propose will depend on factors that lead the language engineer to expect differences in one direction or the other. These instances are referred to as one-tailed (one-directional) hypotheses as each predicts a specific way in which there will be a difference between read and spontaneous speech . If the language engineer wants to test for a difference but has no theoretical or empirical reasons for predicting the direction of the difference, then the hypothesis is said to be two-tailed. Here, large differences between the means of the read and spontaneous speech, no matter which direction they go in, might constitute evidence in favour of the alternative hypothesis.
The distinction between one and two-tailed tests is an important one as it affects what difference between means is needed to assert a significant difference (i.e., support the null hypothesis ). In the case of a one-tailed test, smaller differences between means are needed than in the case of two-tailed tests. Basically, this comes down to how the tables are used in the final step of assessing significance (see below). There are no fixed conventions for the format of tables for the different tests, so there is no point in illustrating how to use them. The tables usually contain guidance as to how they should be used to assess significance.
Hypothesis testing involves asserting what level of support can be given in favour of, on the one hand, the null, and, on the other, the alternate hypotheses. Clearly no difference between the means of the read and spontaneous speech would indicate that the null hypothesis is supported for this sample. A big difference between the means would seem to indicate that there is a statistical difference between these samples if the direction in which the means differs is in the same direction as hypothesised for a one-tailed hypothesis or if a two-tailed test has been formulated. The way in which a decision whether a particular level of support (a probability) is provided is described next.
In the read-spontaneous
example that we have been working
through, we are interested in testing for a difference between
means for two samples where, it is assumed, the samples are from
the same speaker. The latter point requires that a related groups
test as opposed to an independent groups test is used (see
Figure 9.1 on page  ). In this case, the
t statistic is computed from:
). In this case, the
t statistic is computed from:
![]()
Thus if the read speech for 15 speakers had a mean tone unit duration of 40.2 centiseconds and the spontaneous speech 36.4 centiseconds and the standard deviation of the difference between the means is 2.67, the t value is 1.42. The t value is then used for establishing whether two sample means lying this far apart might have come from the same (null hypothesis ) or different (alternate hypothesis) distributions. This is done by consulting tables of the t statistic using n/-1 degrees of freedom (here n refers to the number of pairs of observations).
In assessing a level of support for the alternate hypothesis, decision rules are formulated. Basically this involves stipulating, assuming that the samples are from the same distribution, that if the probability of the means lying this far apart is so low then a more likely alternative is that the samples are drawn from different populations. The ``stipulation'' is done in terms of discrete probability levels and, conventionally, if there is a less than 5% chance that the samples were from the same distribution, then the hypothesis that the samples were drawn from different distributions is supported (the alternative hypothesis at that level of significance). Conversely, if there is a greater than 5% chance that the samples are from the same distribution, the null hypothesis is supported. In the worked example, with 14 degrees of freedom, a t value of 1.42 does not support the hypothesis that the samples are drawn from different populations, thus the null hypothesis is accepted.
It should be noted that support or rejection of these alternative hypotheses is statistical rather than absolute. In 1/20 (5%) cases where no difference is asserted, a difference does occur (referred to as a Type II error, accepting the null hypothesis when it is false) and in cases where a 5% significance level is adopted and differences found, 1 occasion out of 20 will also lead to an error (referred to as a Type I error, rejecting the null hypothesis when it is in fact true).
This chapter of the Handbook does not cover all statistical tests that might be encountered, only offer a background and point to relevant material. However, some comments on Analysis of Variance (ANOVA) are called for as it is a technique that has a widespread use in language engineering.
ANOVA is a statistical method for assessing the importance of factors that produce variability in responses or observations. The approach is to control for a factor by specifying different values (or, treatment levels ) for it in order to see if there is an effect. It can be thought of as having sampled a potentially different population (different in the sense of having different means). Factors that have an effect change the variation in sample means, where ``factor'' refers to a controlled independent variable . When the experimenter controls the levels of the factors , this is referred to as treatment level .
For example, in the ANOVA approach, two estimates of the variances are obtained: the variance between the sample means, between groups variance , and the variance of each of the scores about their group mean, within groups variance . If the treatment factor has had no effect, then variability between and within groups should both be estimates of the population variance. So, as discussed earlier when the ratio of two sample variances from the same population was considered, if the F ratio of between groups to within groups is taken, the value should be about 1 (in which case, the null hypothesis is supported). Statistical tables of the F distribution can be consulted to ascertain whether the F ratio is large enough to support the hypothesis that the treatment factor has had an effect resulting in larger variance of the between group to the within group means (the alternative hypothesis is supported). Another way of looking at this is that the between groups variance is affected by individual variation of the units tested plus the treatment effect whereas the within groups estimate is only affected by individual variation of the units tested.
ANOVA is a powerful tool which has been developed to examine treatment effects involving several factors . Some examples of its scope are that it can be used with two or more factors. Factors that are associated with independent and related groups can be tested in the same analysis, and so on. When more than one factor is involved in an analysis, the dependence between factors (interactions) comes into play and has major implications for the interpretation of results. A good reference covering many of the situations where ANOVA is used is [Winer (1971)]. Though statistical texts cover how the calculations are performed manually, these days the analyses are almost always done with computer packages. The packages are easy to use if ANOVA terminology is known. Indeed the statistical manuals for these programmes (such as MINITAB, SPSS and BMDP) are important sources which discuss how to choose and conduct an appropriate analysis and should be consulted.
Parametric tests cannot be used when discrete, rather than continuous, measures are obtained since the Central Limit Theorem does not approximate the normal distribution in these instances. The distinction between discrete and continuous measures is the principal factor governing whether a parametric or non-parametric test can be employed. Continuous and discrete measures relate to another taxonomy of scales - interval, nominal and ordinal: interval scales are continuous and the others are discrete. Statisticians consider this taxonomy misleading, but since it is frequently encountered, the nature of data from the different scales is described. Interval data are obtained when the distance between any two numbers on the scale are of known size and is characterised by a constant unit of measurement. This applies to physical measures like duration and frequency measured in Hertz (Hz) which have featured in the examples discussed to now. Nominal scales are obtained when the measures are obtained from symbols to characterise objects (such as sex of the speakers). Ordinal scales give some idea of the relative magnitude of units that are measured but the difference between two numbers does not give any idea of the relative size. The examples discussed below in connection with Likert scales represent this level of measurement.
In cases where parametric tests cannot be used, non-parametric (also known as distribution-free) tests have to be employed. The computations involved in these tests are straightforward and covered in any elementary text book [Siegel (1956)]. A reader who has followed the material presented thus far should find it easy to apply the previous ideas to these tests. To help the reader access the particular test needed in selected circumstances (parametric and non-parametric), a tree diagram for the different decisions it is necessary to make is given in Figure 9.1. Thus, a particular test might require a number of judges to indicate how acceptable they think the synthesiser output is from before to after a change has been made. The dependent variable is the frequency of judges considering whether the synthesiser produced satisfactory output or not before and after the change; for this, a McNemar test is appropriate.
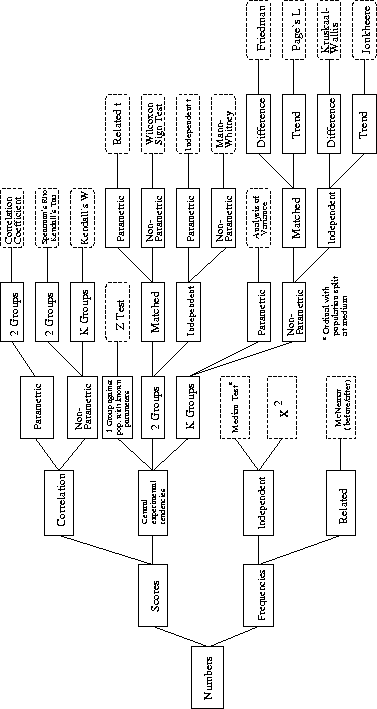
Figure 9.1: Summary of decision structure for establishing what statistical test to use for data
A number of representative questions a language engineer might want to answer were considered at the start of this section. Let us just go back over these and consider which ones we are now equipped to answer. First there was how to check whether there are differences between spontaneous and read speech.
If the measures are parametric (such as would be the case for many acoustic variables), then either an independent or related t test would be appropriate to test for differences. An independent t test is needed when samples of spontaneous speech and read speech are drawn from different speaker sets; a related t test is used when the spontaneous and read samples are both obtained from the same group of speakers.
If the measures are non-parametric (e.g. ratings of clarity for the spontaneous and read speech) then a Wilcoxon test would be used when the read and spontaneous versions of the speech are drawn from the same speaker and a Mann-Whitney U test otherwise.
If you find differences between read and spontaneous speech that require them to use the latter for training data (see application described), how can you check whether language statistics on your sample of recordings is representative of the language as a whole - or, what might or might not be the same thing, how can you be sure that you have sampled sufficient speech? For this, the background information provided to estimate how close sample estimates are to population estimates is appropriate.
The next questions in our list given in the introduction lead on to the second major theme which we want to cover: the general principles behind setting up a well-controlled experiment . The particular experiments that will be considered concern the assessment of the procedures for segmenting and labelling the speech for training and testing the ANNs . The discussion concerning experimental design, etc. will apply to many more situations, however. Once we have an idea what the experimental data would look like, we can consider how to treat the data statistically, which involves hypothesis testing again.