System dimension configuration

It is important for telephone applications to determine the number of ports required with respect to the ``call volume '' and the type of information to be delivered. The method of dimensioning system capacity  is based on the procedure conducted in the management of call handling resources. It is based on the likely maximum number of calls during the traffic peak period and the average duration  of the calls. Of course the number of calls per hour considered here is an average figure and may depend on the activity (opening hours, promotion events, etc.). It may change slightly or significantly with independent external events. Thus, the system is sized to support an average number of calls and to lose a minimum of them.

The system may offer a shared resource architecture based on an internally switched access to the required voice processing resource (recognition  and/or synthesis ) on an as needed basis. In that case one may have fewer recognisers than lines but should apply the following computation to know how many calls will not be satisfied if all resources will be engaged.

1. The first parameter is the number of calls/hour. This has to be computed regarding the calls distribution and considering the busiest hour.
2. The second parameter is the average call length, which determines the duration  of a communication between the application and the caller. It is correlated to the application purpose and its design (message length, cut-through facility,  etc.). One may imagine that users carry out a simple information query as well as a complete transaction (a simple one as well as more complex ones). One also has to account for exits that occur usually during the greeting message (people dialling a wrong number or expecting a human operator). So the average call length is computed on the basis of several experiences to minimise inconsistencies and to account for a weighting factor for each type of the scenarios  mentioned above (abandon, simple transaction, complex ones).

This computation leads to the complete average call length and the number of calls during the peak period that should be handled by the system.

The Erlang  is the measure unit that defines the system dimensions. This measure is given by tables showing the number of ports as a function of the percentage of calls that will be lost The table is called the Erlang B carried-traffic table (see Table 2.5 on page ).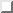

The unit is defined as follows:

Erlang = length in seconds

It is obvious that one cannot - especially for economic reasons - provide resources large enough to handle all the calls. It has to be clear that some calls will not be satisfied and will be lost. There is an optimal balance to look for which is a compromise between the number of lost calls and the cost of extra telephone ports. The percentage of lost calls is referred to as the blockage level .

Let us assume that during the busiest hour the application should respond to 240 simultaneous calls and that the average call length (the average duration  of a call) is 180s.

1/3600 240 180 = 12 Erlangs.

If one accepts losing one call out of ten (10%), then the closest value in the table to 12 is 11,47, which indicates that the required number of ports is 14.

If one accepts losing only one call out of a thousand (0,1%), then the Erlang  table indicates that the closest value is 11,52 and the system should have 23 ports.

Another example: if the number of calls is 480 instead of 240 (two times more) then: to lose less than 10% one needs 26 ports and to loose less than 0,1% one needs 39 ports.