Progress

The prerequisite for assessing progress is an adequate measure of the errors the recogniser produces and how these reduce over time. Unfortunately, it is not a simple matter to derive a measure of error performance.

As already mentioned, some measures of recognition performance mix up errors of segmentation  and classification. Thus, one common kind of list of the types of events that might occur when comparing a human judge's labels with a machine's are:

CORRECT: Phoneme  A occurred at that point according to the transcription  and an A was reported during recognition at that point too.

SUBSTITUTION (MISMATCH): Phoneme  A occurred at that point according to the transcription  but something other than an A was recognised.

DELETED : Phoneme  A occurred at that point according to the transcription  but nothing was reported (not an A nor anything else). This is usually treated as a special subclass of mismatches. However, it could be due to a segmentation  rather than a classification error.

INSERTED : The transcription  would lead one, say, to expect two phonemes  to occur in some stretch of speech but three (including an A) were recognised. The remaining two phonemes  can be aligned with the transcription  so it appears that an A was inserted.

But it is not possible to decide whether deleted  and inserted  phonemes  are instances of segmentation  or classification errors: a human judge might label  a portion of speech as an affricate  whereas the machine might indicate a plosive plus fricative . If the machine had used the same segment boundaries as the human, performance might have been equivalent.

The simplest type of error measure is the number of phonemes  that the recogniser correctly recognises compared with the number the human judges correctly recognise. A basic (unresolved) problem for this measure is that if humans cannot provide ``perfect'' classifications, the machine may be receiving noisy data . Specifically in connection with assessing accuracy  of classification, for example, the problem is what is the ``correct'' answer for phones  that subjects do not agree on. This raises another issue specifically in connection with a particular technique that has been applied for assessing recognisers. The technique is signal detection theory (SDT)  and the technique will first be outlined before problems in applying it to assess recognisers (both humans and machines) are discussed.

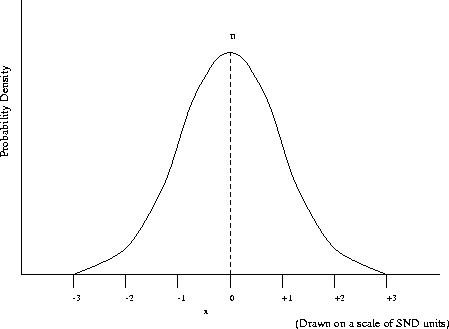
The basic idea behind SDT  is that errors convey information concerning how the system is operating (in this respect, it is an advance on simple error measures). In the signal detection theory model, it is assumed that there is a distribution of activity associated with the event to be detected (e.g. recognition of phoneme A ). The recogniser is performing according to some criterion such that if activity is above the criterion, the recogniser (which can be a human or a machine) reports that the phoneme  is present and below the criterion, subjects report that the phoneme  did not occur. Usually, the threshold is set so that most but not all activity associated with a signal leads to that phoneme  being recognised. Activity associated with the signal distribution above the criterion threshold results in signals being detected (hit) and those below are ``missed''. This is shown in Figure 9.2.

 
Figure 9.2: Activity associated with signal distribution 

The abscissa is activity level and the distribution (in terms of Standard Normal Deviate units) represents the probability distribution of events associated with the signal (phoneme A ) at the various activity levels. The signals associated with other phones  are ``noise '' in relation to the phoneme  and they give rise to a distribution of noise  activity which influences recognition . The noise distribution represents the probability distribution of activity levels and the criterion activity level is the same as that applied to the signal distribution. Most of the noise distribution on processes associated with good recognisers will be below the criterion but some will be above. When activity associated with the noise  distribution below the criterion is encountered, subjects correctly reject this activity as being associated with phoneme  A whilst when it is above this criterion, they incorrectly report a signal to have occurred - referred to in signal detection theory  as a false alarm . This is shown in Figure 9.3.

The criterion is at the same activity level in each case, so the figures combine to give a complete model of the recognition process (see Figure 9.4).

 
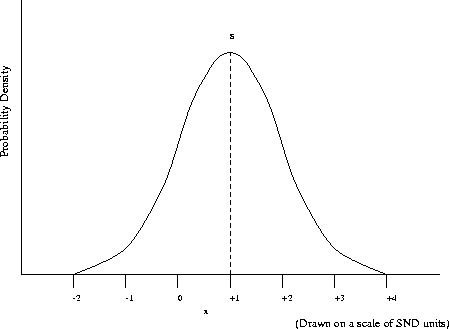
Figure 9.3: Activity associated with noise distribution 

 
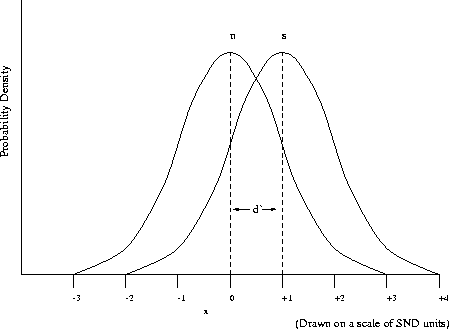
Figure 9.4: Activity level associated with signal and noise distribution 

The error classes described earlier are associated with the categories needed for a signal detection analysis as follows:

HITS = correct

FALSE ALARMS = False + insertions 

MISSES = Mismatch + deleted 

CORRECT REJECTIONS  = total phonemes  - (correct + false + mismatch + deletions )

With the data available in the form of frequency counts of these categories, standard methods can be employed to ascertain (a) the separation between the mean of the noise  and signal distributions and (b) the decision criterion that has been applied. These are referred to as d' and respectively; d' is particularly important in the present context as it is a measure of the discriminability of the signal distribution from the noise  distribution which takes into account all the error information available. A work sheet of the calculations of d' and and tables needed for the calculation are included as Appendix 1.

A way in which the effects of changing the criterion can be seen is by plotting the relationship between hits and false alarms.The trading relationship is referred to as a Receiver Operating Characteristic (ROC) .

The problem alluded to earlier in connection with SDT is distinguishing between what is signal and what is noise . In earlier work it has been assumed that human judges are capable of providing the ``correct'' answers. However, agreement between judges is notoriously low even for gross classifications (for instance, in the stuttering   literature, inter-judge agreement about stutterings is as low as 60% for expert judges). The finer level of classification called for here would lead one to expect that agreement about phone  classes would also be low.

Possible ways out of this dilemma are (1) improvement in psychophysical procedures and (2) (related) normalisation procedures across judges to obtain some composite level of agreement.