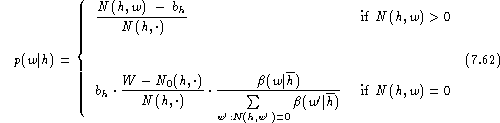
The basic idea is to subtract a constant value from the counts of the observed events. Thus we define the model for absolute discounting and backing-off:
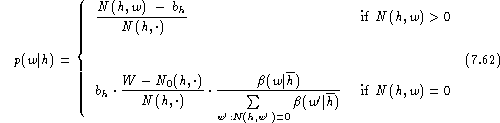
Using the same manipulations as for linear discounting , i.e. separating the singletons, ordering and carrying out the sums, we have for the leaving-one-out log-likelihood function:
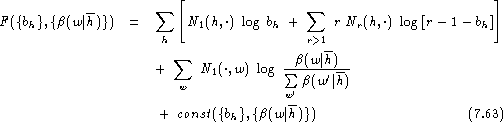
For the backing-off distribution ![]() ,
we obtain the same equation as for linear discounting.
For the discounting parameter
,
we obtain the same equation as for linear discounting.
For the discounting parameter ![]() ,
we obtain the following equation after separating the term with
r=2:
,
we obtain the following equation after separating the term with
r=2:
![]()
For this equation, there is no closed-form solution. We will
derive an upper and a lower bound for ![]() .
Obviously, the right hand side is always greater than or equal to zero,
and thus we get the upper bound:
.
Obviously, the right hand side is always greater than or equal to zero,
and thus we get the upper bound:
![]()
Lower bounds are obtained by observing the inequalities
![]()
Using the additional inequality
![]() ;
we have the lower bound:
;
we have the lower bound:
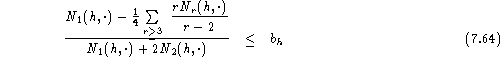
Using the inequality
![]()
this can be simplified to the more convenient bound:
![]()