In this section, we will consider structures that allow us to define classes (or categories) for words that exhibit similar behaviour in the context of language modelling. Word classes or parts of speech (POS) can be viewed as an attempt to cope with the problem of sparse data in language modelling [Derouault & Merialdo (1986)]. Typically, these word classes are based on syntactic-semantic concepts and are defined by linguistic experts. Generalising the concept of word similarities, we can also define word classes by using a statistical criterion, which in most cases is, but does not have to be, maximum likelihood [Jelinek et al. (1990), Jelinek (1991), Brown et al. (1992), Ney et al. (1994)].
There are two levels at which we will introduce equivalence
concepts: the level of word histories h and the level of
single words w. In a sequence of training data ![]() ,
the history of word
,
the history of word ![]() is given by the most recent M words
is given by the most recent M words
![]() .
The equivalence classes of the possible word histories h
for a word w will be
called states and denoted by
a so-called
.
The equivalence classes of the possible word histories h
for a word w will be
called states and denoted by
a so-called
For both the states s and the word classes g,
we define new counts:
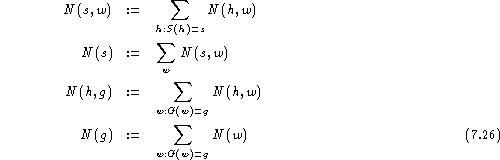
Using only the history mapping ![]() , we have the probability model:
, we have the probability model:
![]()
with the log-likelihood function:
![]()
Here, as usual, the symbol p(.) denotes a more specific model
as opposed to Pr(.).
Plugging in the relative frequencies as estimates for
p(w|s) = N(s,w)/N(s),
we obtain:
![]()
This criterion has the form of an entropy, which also
arises in the context of hierarchical equivalence classes
and CART [Bahl et al. (1989), Breiman et al. (1984)],
where a tree structure is
imposed on the mapping S.
In contrast, here no hierarchical structure is imposed on the word classes
so that no special structure for the mapping
![]() is assumed.
By using equivalence states, we can reduce the number of free parameters:
is assumed.
By using equivalence states, we can reduce the number of free parameters:
![]() in comparison with
in comparison with ![]() for a bigram model
and
for a bigram model
and ![]() for a trigram model, where |S| is the number of
equivalence states.
However, these numbers are somewhat artificial, because even for
large text databases, the number of really independent parameters
is much smaller.
for a trigram model, where |S| is the number of
equivalence states.
However, these numbers are somewhat artificial, because even for
large text databases, the number of really independent parameters
is much smaller.
When now adding word classes using the mapping ![]() ,
we have to distinguish two types of
probability distribution:
,
we have to distinguish two types of
probability distribution:
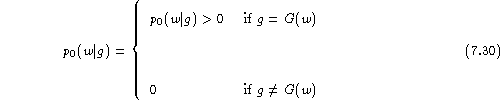
For the probability Pr(w|h),
we then have the decomposition:
![]()
The log-likelihood function now depends on both mappings G and S
and can be written as [Ney et al. (1994)]:
![]()
Plugging in the relative frequencies for p(w), p(s,g),p(s),p(g)
as maximum likelihood estimates, we have:
![]()
A two-sided symmetric model can be defined by using the word
classes both for
the current word and its predecessor words.
For a bigram (v,w), we use ![]() to denote
the corresponding word classes.
For a bigram model, we have then:
to denote
the corresponding word classes.
For a bigram model, we have then:
![]()
The log-likelihood function for such a symmetric
model is easily derived using the equations of the preceding paragraph:
where ![]() denotes the class bigram of the
word bigram (v,w) and
denotes the class bigram of the
word bigram (v,w) and ![]() are
defined in the usual way.
Such a symmetric model leads to a
drastic reduction in the number of free parameters:
are
defined in the usual way.
Such a symmetric model leads to a
drastic reduction in the number of free parameters:
![]() probabilities for the table
probabilities for the table ![]() ;
(W-|G|) probabilities for the table
;
(W-|G|) probabilities for the table ![]() ,
and W indices for the mapping
,
and W indices for the mapping ![]() .
In a similar way, we have for the symmetric trigram model:
.
In a similar way, we have for the symmetric trigram model:
![]()
So far, the assumption has been that the mappings for the
word classes or the equivalence states are known.
Now we describe a procedure by which such mappings can be
determined automatically. This automatic procedure will be
developed for the two-sided symmetric model of Eq.(7.35).
The task is to find a mapping ![]() that assigns
each word to one of |G| different word classes.
Since these classes are found by a statistical
clustering procedure, they are also referred to
as word clusters . The perplexity
of the training data , i.e.
that assigns
each word to one of |G| different word classes.
Since these classes are found by a statistical
clustering procedure, they are also referred to
as word clusters . The perplexity
of the training data , i.e. ![]() ,
is used as optimisation criterion.
In the spirit of decision-directed learning [Duda & Hart (1973), p. 210,], the basic concept of the algorithm
is to improve the value of the optimisation criterion by making
local optimisations, which means moving a word from one class
to another in order to improve the log-likelihood criterion.
Thus we obtain the algorithm shown in Table 7.5.
,
is used as optimisation criterion.
In the spirit of decision-directed learning [Duda & Hart (1973), p. 210,], the basic concept of the algorithm
is to improve the value of the optimisation criterion by making
local optimisations, which means moving a word from one class
to another in order to improve the log-likelihood criterion.
Thus we obtain the algorithm shown in Table 7.5.
More details on this algorithm and related ones can be found in [Brown et al. (1992)] and [Ney et al. (1994)]. For small amounts of training data , such automatically determined word classes may help to reduce the perplexity of a word based bigram or trigram language model [Brown et al. (1992), Ney et al. (1994)].