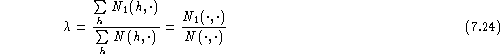



Next: Cache
Up: Multilevel smoothing for trigram
Previous: The full trigram model
In smoothing trigram models by linear discounting or interpolation ,
the smoothing parameters,
both 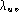 and
and 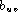 , have been assumed
to depend on the word pair uv.
The number of these word pairs itself is huge so that
reducing the number of smoothing parameters is desirable.
Often, the parameters are pooled or tied
across different histories by setting [Jelinek & Mercer (1980)]:
, have been assumed
to depend on the word pair uv.
The number of these word pairs itself is huge so that
reducing the number of smoothing parameters is desirable.
Often, the parameters are pooled or tied
across different histories by setting [Jelinek & Mercer (1980)]:
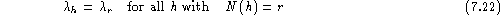
This means that the parameters are tied across histories h with
the same count N(h).
It is straightforward to repeat the derivations
for this type of tying.
As result, we obtain:

Similarly, when assuming the parameters to
be independent of the histories h, we obtain:
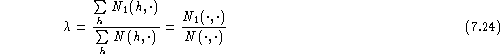
For absolute discounting , we obtain similar formulae in
the case of tying.
In particular for absolute discounting , the experimental results
show that there is no degradation in perplexity when
using history independent discounting parameters [Ney & Essen (1993)].
In a real implementation, no matter whether for off-line purposes
or in an operational prototype system, the
computational complexity of the trigram or bigram model
has to be considered, namely
the memory requirements and the access time.
- To store the trigram and bigram counts, we cannot use a
standard array implementation. Even for a simple model like
a bigram model, it is impossible to store
the full table of conditional probabilities, which
would require
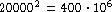 entries for
a vocabulary of 20000 words.
Instead, often a so-called list implementation is used
which works as follows.
For each word w, we have a pointer into the
actual list, and for each observed trigram
(u,v,w), an entry of the list
consists of two parts, namely
the index pair (u,v) and the trigram count N(u,v,w).
For efficiency, this organisation should be combined
with the counts for the bigram models.
A further reduction in memory costs is achieved by
removing the singletons [Katz (1987)] from the list of
seen bigrams and trigrams. In particular, by simply removing
the trigram singletons, the storage costs can be reduced
dramatically without affecting the perplexity much.
We give a specific example for the WSJ corpus
of 39 million running words, for which experimental results
will be described. Here, the storage cost is
126 Mbyte when 4-byte values are used for all pointers
and counts. This storage cost can be reduced down
to 66 Mbyte by omitting the trigram singletons.
entries for
a vocabulary of 20000 words.
Instead, often a so-called list implementation is used
which works as follows.
For each word w, we have a pointer into the
actual list, and for each observed trigram
(u,v,w), an entry of the list
consists of two parts, namely
the index pair (u,v) and the trigram count N(u,v,w).
For efficiency, this organisation should be combined
with the counts for the bigram models.
A further reduction in memory costs is achieved by
removing the singletons [Katz (1987)] from the list of
seen bigrams and trigrams. In particular, by simply removing
the trigram singletons, the storage costs can be reduced
dramatically without affecting the perplexity much.
We give a specific example for the WSJ corpus
of 39 million running words, for which experimental results
will be described. Here, the storage cost is
126 Mbyte when 4-byte values are used for all pointers
and counts. This storage cost can be reduced down
to 66 Mbyte by omitting the trigram singletons.
- For fast access to the bigram and trigram lists,
we have to use suitable techniques, e.g. binary
search . Short term storing of language probabilities might also
be appropriate, depending on the interaction between
language model and search .




Next: Cache
Up: Multilevel smoothing for trigram
Previous: The full trigram model
EAGLES SWLG SoftEdition, May 1997. Get the book...