Strictly speaking,
to evaluate the quality of a stochastic language model,
we would have
to run a whole recognition experiment. However, as a first approximation,
we can separate the two types of probability distribution in
Bayes' decision rule and confine ourselves
to the probability that the language
model produces for a sequence of (test or training) words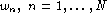 
.
To normalise this prior probability with respect to the number N
of words, we take the Nth root and take the inverse to
obtain the so-called corpus (or test set )
perplexity perplexity [Bahl et al. (1983)]:
Inserting the decomposition into conditional probabilities of Eq.(7.2)
and taking the logarithm, we obtain:
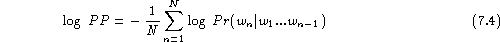
To avoid confusions, we prefer the term ``corpus perplexity ''
because it can be used for both training and test data.
The above equations show that the corpus perplexity is the
geometric average of the reciprocal probability over all N words.
Apart from the constant factor (-1/N), the corpus perplexity
is identical to the average conditional probability or likelihood.
Therefore minimising the corpus perplexity is the same as
maximising the log-likelihood function.
The perplexity measures the constraints expressed by the language model. From the viewpoint of the recognition task, we can say that the language model reduces the number of word choices during the recognition process. Thus the perplexity can be interpreted as the average number of word choices during the recognition process. As a first approximation, the perplexity measures the difficulty of a recognition task: the smaller the perplexity, the lower the error rate . For example, depending on the application and the language model, a recognition system with a vocabulary of 1000 words can have such strong language constraints that the recognition task is easier than digit recognition. This was true for all of the early speech recognition systems like HARPY and HEARSAY [Lea (1980)]. A special aspect in the definition of corpus perplexity should be noted. If a word in the corpus is assigned a probability of zero by the language model, the perplexity will be infinitely large. This is one of the real challenges for the language model: the prediction of the next word should be as good as possible without excluding any of the words of the vocabulary.
In some articles, the authors relate perplexity to entropy as used in information theory [Bahl et al. (1983)]. There the assumption is that the underlying probability distribution of the language model is exactly known. However, for practical comparisons, so-called test set perplexity or corpus perplexity is more useful.