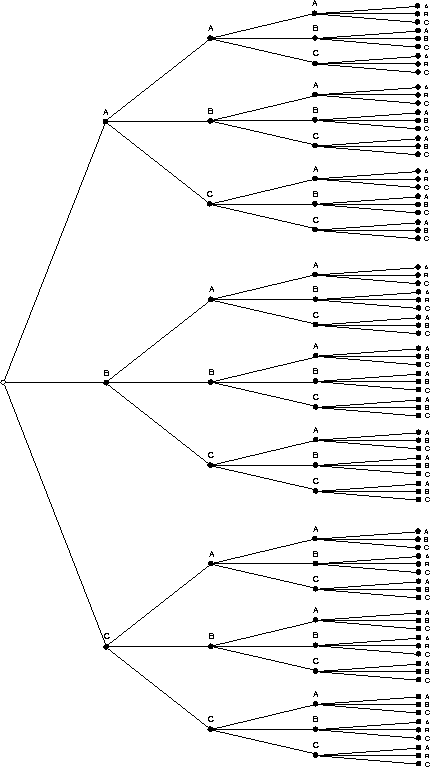
Figure 7.2: Illustration of the decision problem for a three-word vocabulary
The task of a language model is to express the restrictions imposed on the way in which words can be combined to form sentences. In other words, the idea is to capture the inherent redundancy that is present in the language, or to be more exact, in the language subset handled by the system. This redundancy results from the syntactic, semantic and pragmatic constraints of the language and may be modelled by probabilistic or non-probabilistic (``yes/no'') methods. For a vocabulary of three words A,B,C, Figure 7.2 illustrates the situation. What is always possible is to arrange the word sequences in the form of a tree. Figure 7.2 shows the sentence tree for all four-word sentences. Now some of these word sequences may be impossible, some may be possible, and others may be very typical according to syntactic and semantic and maybe pragmatic constraints. The task of the language model is now to express these constraints by assigning a probability to each of the sentences. In simple cases like voice command applications, it might be sufficient to just remove the illegal sentences from the diagram and compress it into a finite state network .

Figure 7.2: Illustration of the decision problem for a three-word vocabulary
For large vocabulary recognition tasks,
such methods cannot be used because we have to allow
any word sequence types, which is difficult to
describe deterministically.
The task of a stochastic language model
stochastic language model
is to provide
estimates of these prior probabilities ![]() . Using the
definition of conditional probabilities, we obtain the decomposition:
. Using the
definition of conditional probabilities, we obtain the decomposition:
![]()
Strictly speaking, this equation requires a suitable
interpretation of the variable N, the number of
words. When considering a single sentence,
the number of words is a random variable itself,
and we need an additional distribution over the sentence lengths.
In practice, the problem is circumvented by applying the above
equation to a whole set of sentences and
extending the vocabulary by a special symbol (or ``word'') that
marks the end of a sentence (and the beginning of the next sentence).
For large vocabulary speech
recognition, these
conditional probabilities are typically used in the following
way [Bahl et al. (1983)].
The dependence of the conditional probability of observing a word
![]() at a position n is modelled as being restricted to its
immediate (m-1) predecessor words
at a position n is modelled as being restricted to its
immediate (m-1) predecessor words ![]() .
The resulting model is that
of a Markov chain and is referred to as m-gram model.
m-gram model
The following types of model are quite common:
.
The resulting model is that
of a Markov chain and is referred to as m-gram model.
m-gram model
The following types of model are quite common:
It is obvious that, apart from speech recognition, language models are also essential for optical character recognition [Mori et al. (1992)] and language translation [Berger et al. (1994)]. It is interesting to mention that similar m-gram techniques are used in the context of acoustic-phonetic modelling. The main difference is the level at which the statistical data are collected, i.e. at the level of phonemes or the level of phones, which are the acoustic realisations of the phonemes . Phone bigrams and trigrams are referred to as diphones and triphones , respectively. Statistical techniques related to those used in language modelling can also be applied to language understanding [Pieraccini et al. (1993)].