Due to the smoothing techniques, bigram and trigram language models are robust and have been successfully used more widely in speech recognition than conventional grammars like context free or even context sensitive grammars. Although these grammars are expected to better capture the inherent structures of the language, they have a couple of problems:
When using context free grammars , the terminals or symbols that can be observed are the words of the vocabulary [Lafferty et al. (1992), Wright et al. (1993), Della Pietra et al. (1994), Yamron (1994)]. We use the notation:
;
: an arbitrary nonempty string of terminals and non-terminals.
We typically attach probabilities
to the context free rules.
For a production rule like
we have a conditional probability 
that a given
non-terminal A will be rewritten as . As usual, these
probabilities must be normalised:
As usual in the framework of
context free grammars , one often uses so-called normal
forms like Chomsky and Greibach normal form
for which standard introductions to formal languages in compiler construction
theory can be consulted.
Typically, these normal forms simplify the
analysis of the problem under consideration,
and there are automatic techniques for converting arbitrary
context free grammars into these normal forms.
For each parse tree of a given string, we can compute its probability as the product over all its production rules. The probability of the given word string is then obtained by summing these probabilities over all possible parse trees. The fundamental definitions for context free grammars are well covered in textbooks [Fu (1982), Gonzalez & Thomason (1978)].
For the application of stochastic context free grammars, stochastic grammar we consider four questions or problems:
,
how can we compute the conditional probability
for the word 
in position n:
The main stumbling block in using grammar based language models so far seems to be that the grammar rules as such are not available, either because handwritten grammars are simply not good enough or because the problem of grammatical inference is too big. To mitigate these problems, there have been attempts to use special types of context free grammars which are referred to as lexicalised or link grammars. Their non-terminals are assumed to depend on the words of the lexicon. These grammars include the bigram and trigram language models as special cases and thus provide a smooth transition from the m-gram language models to context free grammars [Lafferty et al. (1992), Della Pietra et al. (1994), Yamron (1994)]. Although so far there are only preliminary results, we will consider these approaches in more detail because they offer promising extensions from m-gram models and they provide a good framework to show the relationship between m-gram language models, finite state grammars and context free grammars.
To describe this type of grammar, we will use
a special version of the Greibach
normal form. Each context free grammar can be
converted into a grammar whose rules are of the following three types:
The third rule type describes a branching process,
which is required for the full power of context free grammars.
Without it, we are restricted to regular grammars which
can be conveniently represented by finite state networks.
Each network state is identified with a non-terminal of
the grammar.
To obtain a bigram language model in this framework, we
use a separate non-terminal 
for each word w.
The bigram model itself is expressed by
the following rule type for the word pair (vw):
The bigram rules can be represented as a finite
state network as
illustrated in Figure 7.5 for
a given word sequence.
Unlike the conventional representation, the
nodes stand for the observed words, i.e. the terminals,
whereas the links represent the non-terminals.
For a complete description of the grammar,
we have to include the rules for sentence begin and end.
For a trigram model, we have to use a separate non-terminal
for each word pair (vw), and the rules depend on
the word triples (uvw):
The trigram rules are illustrated in Figure 7.6.
Figure 7.5: Bigram as a finite state grammar
Figure 7.6: Trigram as a finite state grammar
To go beyond the power of m-gram and finite state
language models ,
we need more than one non-terminal
on the right-hand side.
To simplify the presentation, we restrict ourselves
to the special case of pairwise word dependencies,
which can be viewed as an extended bigram model.
In addition to the standard
bigram non-terminals now denoted by 
, we have
additional non-terminals for the branching process,
which are denoted by 
for word w:
The production rule for non-terminal is different from
the rules for and, for example, could have this form:
This type of rule is capable of handling long range dependencies
sich as those in the following English examples
[Della Pietra et al. (1994)]:
A conventional bigram or trigram language model cannot
capture these dependencies.
In general, for a given word string,
context free grammars define a hierarchical structure
by the parsing process.
Figure 7.7 shows the parsing structure in the conventional
form. There is another equivalent representation
shown in Figure 7.8, where the long range dependencies
are expressed by special links in addition
to the short range (i.e. next neighbour) bigram links.
In this link representation, the three
different types of rule can be seen as follows.
The step rule stands for the standard bigram link
to the next right word.
The branch rule has two links: in addition to the
bigram link, there is a long range link to another
word, e.g. the link from word 
to 
in Figure 7.8.
Since there is the long range link for word ,
there is no bigram link for , and therefore
the halt rule must be used for word 
,
the predecessor of .
For this type of grammar based language model, there are
only some preliminary experimental results [Della Pietra et al. (1994), Yamron (1994)].
A still existing problem is the question of
how to select the relevant word links in view
of the large number of possible spurious links.
In [Della Pietra et al. (1994)], a method has been suggested for
inferring the links automatically from a text corpus.
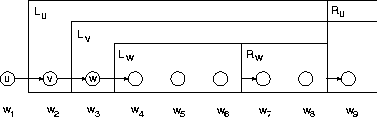
Figure 7.7: Parsing in the conventional form
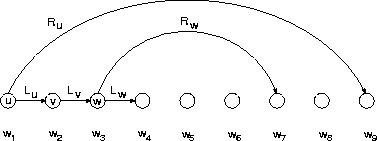
Figure 7.8: Parsing in link grammar form