Every approach to automatic speech recognition is faced with the problem of taking decisions in the presence of ambiguity and context, and of modelling the interdependence of these decisions at various levels. If it were possible to recognise phonemes (or words) with a very high reliability, it would not be necessary to rely heavily on delayed decision techniques, error correcting techniques and statistical methods. In the near future, this problem of reliable and virtually error free phoneme or word recognition without using high-level knowledge is unlikely to be solved for large-vocabulary continuous-speech recognition. As a consequence, the recognition system has to deal with a large number of hypotheses about phonemes , words and sentences, and ideally has to take into account the ``high-level constraints'' as given by syntax , semantics and pragmatics . Given this state of affairs, statistical decision theory tells us how to minimise the probability of recognition errors [Bahl et al. (1983)].
The word sequence 
to be recognised from the sequence of
acoustic observations 
is determined as that word sequence
for which the posterior probability
attains its maximum.
The sequence of acoustic vectors
over time t=1...T
is derived from the speech signal in the
preprocessing step of acoustic analysis.
Statistical decision theory leads to the so-called
Bayes decision rule, which can be written in the form:
where 
is the conditional probability,
given the word sequence
,
of observing the sequence of acoustic vectors and
where 
is the prior probability of producing the word
sequence .
The application of the Bayes decision rule
to the speech recognition problem is illustrated in
Figure 7.1.
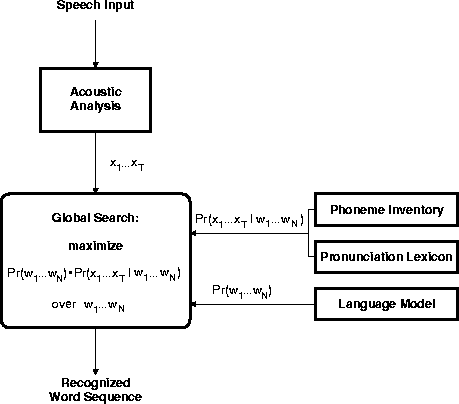
Figure 7.1: Bayes decision rule for speech recognition
The decision rule requires two types of probability distribution, which we refer to as stochastic knowledge sources, along with a search strategy:
,
is independent of the acoustic
observations; its task
is to incorporate restrictions on the way
in which the words of the vocabulary can be concatenated
to form whole sentences.
,
is the conditional probability of observing
the acoustic vectors when the speaker utters the words
. Like the language model probabilities,
these probabilities are estimated during the training
phase of the recognition system . For a large vocabulary
system,
there is typically a set of basic recognition units that are
smaller than whole words. Examples of these so-called subword
units are phonemes ,
demisyllables or syllables .
Often, context dependent phoneme units
are also used, for example so-called triphones, i.e.\
phoneme units in a triphone context.
The word models are then obtained by concatenating the subword models
according to the phonetic transcription of the words in a
pronunciation dictionary .
In most systems, the acoustic-phonetic models
are based on Hidden Markov models
[Levinson et al. (1983), Bahl et al. (1983)].