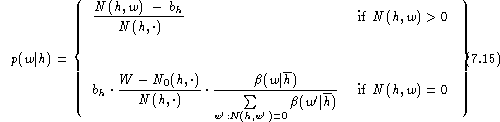
The basic idea is to subtract a constant from all counts r>0 and thus, in particular, to leave the high counts virtually intact. The intuitive justification is that a particular event that has been seen exactly r times in the training data is likely to occur r-1, r or r+1 times in a new set of data. Therefore, we assume a model where the counts r are modified by an additive offset. From the normalisation constraint, it immediately follows that this must be a negative constant since the unseen events require a non-zero probability. Experimental results in [Ney & Essen (1993)] show that the resulting estimates are close to estimates obtained from the Turing-Good formula after suitable smoothing [Good (1953), Nadas (1985)]. We define the model for absolute discounting:
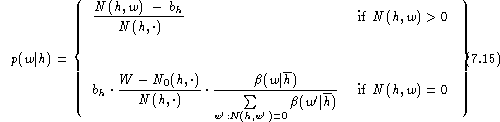
We do the same manipulations as for linear
discounting , i.e. separating the singletons,
ordering and carrying out the sums.
For 
, we obtain the same equation
as for linear discounting .
For the 
dependent part,
we obtain the following
leaving-one-out log-likelihood function:
Taking the partial derivatives with respect to ,
we obtain the following equation after separating the term with
r=2:
For this equation, there is no closed-form solution.
However, there are upper and lower bounds.
As shown in the appendix, we have the upper bound:
and the lower bound:
