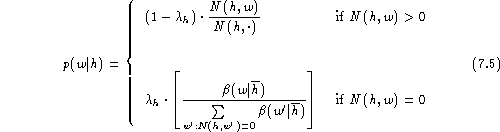
We start with linear discounting in the so-called backing-off model [Katz (1987), Jelinek (1991)]. This model is exceptional in that it allows virtually closed-form solutions in conjunction with leaving-one-out . Thus we can discuss all the important formulae of the approach without recourse to numeric calculations. The model is defined by the equation:
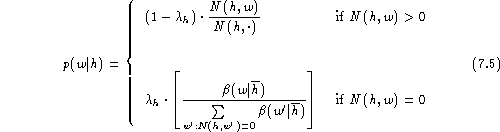
It is easy to verify that the probabilities p(w|h) sum up to unity.
In particular, ![]() is the total probability mass to be distributed over
the unseen words for a given history h:
is the total probability mass to be distributed over
the unseen words for a given history h:
![]()
Here we have two types of parameter sets to be estimated:
The unknown parameters in the discounting models will be determined with the so-called leaving-one-out method. leaving-one-out This method can be obtained as an extension of the cross-validation or held-out method [Duda & Hart (1973), Efron & Tibshirani (1993)], where the training text is split into two parts: a ``retained" part for estimating the relative frequencies and a ``held-out" part for estimating the optimal interpolation parameters. Here, the training text is divided into (N-1) samples as the ``retained" part and only 1 sample as the ``held-out" part; this process is repeated N times so that all N partitions with 1 ``held-out" sample are considered. The basic advantage of this approach is that all samples are used both in the ``retained" part and in the ``held-out" part and thus very efficient exploitation of the training text is achieved. In particular, singleton events are reduced from 1 to 0 so that the effect of not seeing events is simulated.
The application of leaving-one-out to the problem
under consideration is as follows.
By doing some elementary manipulations as shown in the appendix,
we can decompose the log-likelihood
function into two parts, one of which depends only on ![]() and the
other depends only on
and the
other depends only on ![]() :
:
![]()
The ![]() dependent part is:
dependent part is:
![]()
Taking the partial derivatives with respect to ![]() and equating them to zero, we obtain
the closed-form solution:
and equating them to zero, we obtain
the closed-form solution:
![]()
The same value is obtained when we compute the probability mass of unseen
words in the training data for a given history h:
![]()
The same value is obtained when using the
Turing-Good formula [Good (1953), Nadas (1985), Katz (1987), Ney & Essen (1993)].
This formula is extremely useful when we want to
estimate the total probability for events that were
not seen in the training data. This formula tells us
simply to take the number of singleton events, i.e. ![]() ,
divide it by the total number of events, i.e.
,
divide it by the total number of events, i.e. ![]() ,
and use this fraction as estimate for the probability
of new events. This rule can be applied
at various levels such as single words (unigrams ),
word bigrams and word trigrams .
For example, to check the coverage
of the vocabulary,
we can use this formula to estimate the probability
with which we will encounter words that are not part of the vocabulary,
i.e. that we have not seen in the training data .
,
and use this fraction as estimate for the probability
of new events. This rule can be applied
at various levels such as single words (unigrams ),
word bigrams and word trigrams .
For example, to check the coverage
of the vocabulary,
we can use this formula to estimate the probability
with which we will encounter words that are not part of the vocabulary,
i.e. that we have not seen in the training data .
For the backing-off distribution,
the standard method is to use the relative frequencies
as estimates:
![]()
However, as shown in [Generet et al. (1995)], the leaving-one-out method
can be applied to this task, too.
In the appendix, we show how an approximate solution
is obtained for this case. The resulting estimation
formula is:
![]()
where ![]() is defined as:
is defined as:
![]()
For convenience, we have chosen the
normalisation ![]() .
This type of backing-off distribution will be
referred to as singleton backing-off distribution or
singleton distribution for short.
Considering bigram modelling as a specific example, we see that
the singleton backing-off distribution
takes into account such word bigrams as
``has been'', ``United States'', ``bona fide'' etc.,
where the second word is strongly correlated with the immediate predecessor
word. In these cases, the
conventional unigram distribution tends to overestimate
the corresponding probability in the backing-off distribution.
.
This type of backing-off distribution will be
referred to as singleton backing-off distribution or
singleton distribution for short.
Considering bigram modelling as a specific example, we see that
the singleton backing-off distribution
takes into account such word bigrams as
``has been'', ``United States'', ``bona fide'' etc.,
where the second word is strongly correlated with the immediate predecessor
word. In these cases, the
conventional unigram distribution tends to overestimate
the corresponding probability in the backing-off distribution.