The Multiply Perfect Numbers Page

Introduction

Let σ(n) be the number theoretic function which denotes the sum of all divisors of a natural number n. If σ(n) is an integral multiply of n, then n is denoted as a multiply perfect number or k-fold perfect number (also called multiperfect number or pluperfect number). Call σ(n)/n abundancy (also called index or multiplicity) of n. A multiply perfect number is called proper if its abundancy is > 2. For example consider the divisors of the number 120: 1+2+3+4+5+6+8+10+12+15+20+24+30+40+60+120=σ(120)=σ(2^3*3*5)=σ(2^3)*σ(3)*σ(5)=(1+2+4+8)*(1+3)*(1+5)=15*4*6=360=3*120.
Hence 120 is a 3-fold perfect number.

Status

Abundancy	Count	When last number was discovered	Which was last?	Are all discovered?	Estimated total number
1	1	-	-	yes and proved	1
2	51	2018-12-07	18.5560326	no, there are infinitely many	∞
3	6	<= 1643	3.2049844	yes	6
4	36	<= 1929	4.3351682	yes	36
5	65	<= 1990	5.1744360	yes	65
6	245	1993-05-??	5.6720844	yes	245
7	516	1994-01-09	5.9403364	almost surely yes	~ 515
8	1136	2022-05-22	6.5244184	probably yes	~ 1140
9	2164	2022-06-05	7.1993123	no	~ 2200
10	1710	2022-06-11	7.8125224	no	~ 4500
11	2	2022-09-07	8.2948075	no	~ 10000

In column "Which was last?" the identifier ln(ln(MPN)) is given for those which were verfied by me. I checked these numbers only for those MPNs reported before 2023-01-01.
We have a total of 5932+0 (of which 5880 have an abundancy > 2) known and claimed MPNs until 2022-12-31.
It is extremly probable, that all proper MPNs with abundancy <= 7 are discovered.

Data

Richard Schroeppel's archive of 2094 MPNs built 1995-12-13 .
The collection of 5932 MPNs from 2022-12-31(gziped to 1121 kB) sorted by abundancy and magnitude. It is grown out of Rich's database --- thanks ---, and transformed into a new format, such that each multiply perfect number allocates one line -- an ASCII-text-record terminated by newline -- with all its additional informations in the following (standard) form:
M|ln_ln|rich_id,depth|dpf,tpf|date|name|number|comment
Except of the last field, comment, all other fields are obligatory, but they can be empty, e.g. if the discovery date or person is unknown.

| is a separator character between the fields and is not allowed inside any field.
M indicates the abundancy of the number as a lower case letter, such that the letters a,b,c,d,... correspond to the abundancies 1,2,3,4, ... .
ln_ln gives the decimal value of log_elog_e of the number and is rounded to 7 decimal places after the period. This serves now as a unique identifier to each number, also.
rich_id is Rich's unique identifier for this number which encodes the abundancy appended by the exponents of at most the three primes 2,3,5. These exponents are encoded alternatingly in a 26-base system made up of the letters a-z und a 10-base system made up of the digits 0-9. The letter @ is used if a needed prime exponent is zero in the 26-base system. In the case that this identifier is still ambigious, it is appended by a lower case letter which serves as a counter.
depth indicates the minimal number of successive primes (starting with 2) whose exponents must be given to reconstruct the MPN straight forward (without knowing its abundancy).
dpf indicates the number of different prime factors.
tpf indicates the number of total prime factors.
date gives the year of the first (or independent) discovery in the form YYYY-MM-DD as long as month and day (and year) is known.
name gives the name of the discoverer. Like in the date field, multiple independent discoveries are separated by commas.
number is given in its prime factorization of the form:base1^expo1.base2^expo2.base3^expo3. .... where the basei indicates a prime of an ascending list of primes and the expoi indicates the corresponding nonzero exponent; an exponent value of 1 is omitted together with its preceding ^. In the case of the larger 2-perfect numbers, the odd prime (2^??-1) in the factorization is given as M?? to save space with ?? giving the Mersenne Prime exponent as decimal number.

Search this database of 5932 MPNs
Each search-pattern matches literally, except the wild-characters *,?,!,$ which mean:
* -- arbitrary, maybe empty, sequence of characters
? -- exactly one character
! -- begin of record
$ -- end of record.
Hint: orient on the field separator | or the comma in each record to get easier what you want.

And a further list of multiply perfect numbers sorted only by their factorizations (built from the 5932 MPNs of the master list and gziped 226 kB). It has each line cut down to 120 columns and no discovery information or comments are given. Rich's out-dated indentifier is omitted, but a log₁₀(MPN) is given for traditional reasons.
Finally, here are the (email-extracted and edited to put it syntactically in standard form) 0 claimed new (since the database update) found MPNs which I irregularly append (last change: 2023-01-12). To verify these numbers, three steps must be taken: 1) verify for each number n given in its prime factorization that all factors are really prime numbers, 2) compute σ(n) which envolves the factorization of large numbers and then check n's claimed abundancy 3) and lastly test whether n is really new.

Algebraic Transformations

Let σ(n*X)=k*n*X and σ(n*Y)=k*n*Y, with gcd(n,X)=1=gcd(n,Y), i.e. they have no primes in common. Such a pair (X,Y) is denoted as a substitution. To avoid trivial substitutions, one demands further that prime-powers whose primes occuring in both components have different exponents. This yields: Given integers n, X, Y with gcd(n,X)=1=gcd(n,Y). If n*X is a k-perfect number and X*σ(n*Y)=Y*σ(n*X) -- i.e. X and Y have the same "fractional abundancy" -- holds, then n*Y is a k-perfect number, too. Call the size of a substitution the number of different primes involved.
Moreover there is the case that for a fixed (small) prime k the number n is a k-perfect number and gcd(n,k)=1. Then the number k*n is k+1-perfect! I.e. if n has no prime factor k we can construct a further multiply perfect number of a by 1 increased multiplicity. Below are some components listed for pairs (A,B), (C,D), (E,F), (G,H), (I,J), (K,L), (M,N), (P,Q), (R,S), (T,U) and (V,W):

A = 19^2.127^1.151^0.911^0
B = 19^4.127^0.151^1.911^1
size(A,B) = 4 , k = 4,5,6,7,8,9
[occurs 257 times for the known MPNs]

C = 23^1.37^3.73^1.79^0.137^2
D = 23^2.37^1.73^0.79^1.137^1
size(C,D) = 5 , k = 6,7,8,9
[occurs 21 times for the known MPNs]

E = 13^1.31^2.61^1.83^1.97^0.331^1
F = 13^2.31^1.61^2.83^0.97^1.331^0
size(E,F) = 6 , k = 6,7,8
[occurs 31 times for the known MPNs]

G = 3^10.107^1.137^0.547^0.1093^0.3851^1
H = 3^6.107^0.137^1.547^1.1093^1.3851^0
size(G,H) = 6 , k = 4,5,6
[occurs 31 times for the known MPNs]

I = 5^0
J = 5^1
size(I,J) = 1 , k = 5
[occurs 20 times for the known MPNs]

K = 7^5.17^1.37^1.43^1.67^0.307^0.1063^0
L = 7^8.17^2.37^2.43^0.67^1.307^1.1063^1
size(K,L) = 7 , k = 7
[occurs 9 times for the known MPNs]

M = 7^4.13^4.31^1.43^1.61^1.79^0.97^0.157^0.631^0.30941^1
N = 7^9.13^5.31^0.43^2.61^2.79^2.97^1.157^1.631^1.30941^0
size(M,N) = 10 , k = 5,6,7,8
[occurs 4 times for the known MPNs]

P = 2^38.53^1.59^0.157^0.229^1.8191^1.43331^0.121369^1.3033169^0.715827883^0.2147483647^0
Q = 2^61.53^0.59^1.157^1.229^0.8191^0.43331^1.121369^0.3033169^1.715827883^1.2147483647^1
size(P,Q) = 11 , k = 5,6
[occurs 9 times for the known MPNs]

R = 13^14.139^0.157^1.181^1.191^2.199^1.229^1.397^1.827^0.1163^1.4651^1.8269^0.14197^0.28393^0.30941^1.40493^1.161971^1
S = 13^11.139^1.157^2.181^2.191^1.199^0.229^2.397^0.827^1.1163^0.4651^0.8269^1.14197^1.28393^1.30941^0.40493^0.161971^0
size(R,S) = 17 , k = 9,10
[occurs 2 times for the known MPNs]

T = 3^4.11^3.13^1
U = 3^5.11^1.13^2
size(T,U) = 3 , k = 6
[occurs 8 times for the known MPNs]

V = 5^2.7^2.11^1.31^1.71^0
W = 5^4.7^3.11^2.31^0.71^1
size(V,W) = 5 , k = 6
[occurs 8 times for the known MPNs]

They are as more important, as fewer primes are involved in such a substitution. As larger the smallest prime in such a pair is, as more usefull it is, too. On the other hand, as smaller the quotient of the number of different primes in n to the size of the substitution becomes, as more worthless such a substitution becomes for this n. Therefore we demand arbitrarily that the size of a substitution must be less than the number of different primes in each of the two components. Sadly it looks like that substitutions occur only for mpns with small abundancy as the following table of counts for substitutions of size of at most 12 suggests:

Abundancy	3	4	5	6	7	8	9	10	11
# known mpns	6	36	65	245	516	1136	2164	1710	2
# different subst	0	30	37	283	59	6	2	0	0

Then the number of (different) substitutions of size ≤ 12 is finite and probably all are already discovered.

Historical Development of known MPNs

period / year	Antiquity	Middle Ages	< 1910	< 1915	< 1930	< 1955	< 1980	< 1990	1991	1992	1993	1994	1995
known MPNs	5	35	47	235	347	556	596	611	713	1179	1821	1983	2101
increament	5	30	12	188	112	209	40	15	102	466	642	162	118

period	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013
known MPNs	2335	3051	3259	3464	4501	4997	5040	5050	5147	5189	5222	5245	5271	5287	5301	5303	5307	5311
increament	234	716	208	205	1037	496	43	10	97	42	33	23	26	16	14	2	4	4

period / year	2014	2015	2016	2017	2018	2019	2020	2021	2022
known MPNs	5311	5311	5312	5314	5315	5315	5315	5772	5932
increament	0	0	1	2	1	0	0	457	160

The sign < in the row period means "up to and including" the given year.
The value in the row increament indicates the new known MPNs compared to the previous time-period.

Now a list of the discoverer names follows according to Rich Schroeppel (report him, if you think you aren't credited sufficiently):

Discoverer count period Discoverer count period
Armengaud&Woltman&et.al. 1* 1996 Brown 78 1954
Cameron&Woltman&Kurowski&et.al. 1* 2001 Carmichael 98 1907-1911
Cataldi 2* 1588 Clarkson&Woltman&Kurowski&et.al. 1* 1998
codex-Lat.-Monac.- 1* 1456 Colquitt&Welsh 1* 1988
Cooper&Boone&Woltman&Kurowski&et.al. 2* 2005-2006 Cooper&Woltman&Kurowski&et.al. 1* 2013
Cooper&Woltman&Kurowski&Blosser&et.al. 1* 2016 Cunningham 3 1902
Descartes 9 1638-1639 Dokshitzer&Vasyunin 1 1993
Euclid 4* -275 Euler 1* 1772
Elvenich&Woltman&Kurowski&et.al. 1* 2008 Fermat 11? 1636-1643
Findley&Woltman&Kurowski&et.al. 1* 2004 Flammenkamp 137 1993-2000
Flammenkamp&Woltman 344 2000-2001 Franqui&Garcia 135 1953-1954
Freniclei 3 1638 Gage&Slowinski 3* 1992-1996
Gillies 3* 1963 Gretton 123 1990-1993
Gretton&Schroeppel 5 1991-1992 Hajratwala&Woltman&Kurowski&et.al. 1* 1999
Harrison&Moxham 3 2000 Helenius 1261 1992-1997
Helenius&Schroeppel 16 1993 Hurwitz&Selfridge 2* 1961
in-Mersenne-epoch 4 1639-1643 Jumeau 1 1638
Kapek&Moxham 1 2000 Laroche&Woltman&Blosser&et.al. 1* 2018
Lehmer 5 1901 Lucas 1* 1876
Martinson&Moxham 1 2000 Mason 89 1911
Moxham 1006 1995-2001 Nelson&Slowinski 1* 1979
Nickel&Noll 1* 1978 Noll 1* 1979
Nowak&Woltman&Kurowski&et.al. 1* 2005 Pace&Woltman&Kurowski&Blosser&et.al. 1* 2017
Perrier&Woltman 38 2000 Pervouchine 1* 1883
Poulet 145 1929,1954 Powers 2* 1911-1914
Pythagoras 1* -500 Recorde 1 1557
Riesel 1* 1957 Roberts&Moxham 2 1997
Robinson 5* 1952 Schroeppel 7 1983-1991
Shafer&Woltman&Kurowski&et.al. 1* 2003 Slowinski 3* 1982-1985
Smith&Woltman&Kurowski&et.al. 1* 2008 Sorli&Moxham 27 1997-1998
Sorli&Woltman 9 2000-2001 Spence&Woltman&et.al. 1* 1997
Strindmo&Woltman&Kurowski&et.al. 1* 2009 Toshihiro 1 2017
Tuckerman 1* 1971 Whiteside&Moxham 2 1999
Woltman 2416 1997-2013,2021-2022 Yoshitake 17 1974-1993
The column 'count' counts the discoveries until 2022-12-31 and an asterik * indicates that this person has "only" discovered 2-perfect number(s).

Discoverer	count	period	Discoverer	count	period
Armengaud&Woltman&et.al.	1*	1996	Brown	78	1954
Cameron&Woltman&Kurowski&et.al.	1*	2001	Carmichael	98	1907-1911
Cataldi	2*	1588	Clarkson&Woltman&Kurowski&et.al.	1*	1998
codex-Lat.-Monac.-	1*	1456	Colquitt&Welsh	1*	1988
Cooper&Boone&Woltman&Kurowski&et.al.	2*	2005-2006	Cooper&Woltman&Kurowski&et.al.	1*	2013
Cooper&Woltman&Kurowski&Blosser&et.al.	1*	2016	Cunningham	3	1902
Descartes	9	1638-1639	Dokshitzer&Vasyunin	1	1993
Euclid	4*	-275	Euler	1*	1772
Elvenich&Woltman&Kurowski&et.al.	1*	2008	Fermat	11?	1636-1643
Findley&Woltman&Kurowski&et.al.	1*	2004	Flammenkamp	137	1993-2000
Flammenkamp&Woltman	344	2000-2001	Franqui&Garcia	135	1953-1954
Freniclei	3	1638	Gage&Slowinski	3*	1992-1996
Gillies	3*	1963	Gretton	123	1990-1993
Gretton&Schroeppel	5	1991-1992	Hajratwala&Woltman&Kurowski&et.al.	1*	1999
Harrison&Moxham	3	2000	Helenius	1261	1992-1997
Helenius&Schroeppel	16	1993	Hurwitz&Selfridge	2*	1961
in-Mersenne-epoch	4	1639-1643	Jumeau	1	1638
Kapek&Moxham	1	2000	Laroche&Woltman&Blosser&et.al.	1*	2018
Lehmer	5	1901	Lucas	1*	1876
Martinson&Moxham	1	2000	Mason	89	1911
Moxham	1006	1995-2001	Nelson&Slowinski	1*	1979
Nickel&Noll	1*	1978	Noll	1*	1979
Nowak&Woltman&Kurowski&et.al.	1*	2005	Pace&Woltman&Kurowski&Blosser&et.al.	1*	2017
Perrier&Woltman	38	2000	Pervouchine	1*	1883
Poulet	145	1929,1954	Powers	2*	1911-1914
Pythagoras	1*	-500	Recorde	1	1557
Riesel	1*	1957	Roberts&Moxham	2	1997
Robinson	5*	1952	Schroeppel	7	1983-1991
Shafer&Woltman&Kurowski&et.al.	1*	2003	Slowinski	3*	1982-1985
Smith&Woltman&Kurowski&et.al.	1*	2008	Sorli&Moxham	27	1997-1998
Sorli&Woltman	9	2000-2001	Spence&Woltman&et.al.	1*	1997
Strindmo&Woltman&Kurowski&et.al.	1*	2009	Toshihiro	1	2017
Tuckerman	1*	1971	Whiteside&Moxham	2	1999
Woltman	2416	1997-2013,2021-2022	Yoshitake	17	1974-1993

Abundancy First discovered MPN Is it smallest? Date Discoverer
1 1 yes ancient -
2 6 yes ancient -
3 120 yes ancient -
4 30240 yes ~ 1638 R. Descartes
5 14182439040 yes ~ 1638 R. Descartes
6 34111227434420791224041472000 no 1643 P. Fermat
7 6.9545266398342727... *10^70 no 1902 A. J. C. Cunningham
8 2.34111439263306338... *10^161 no 1929 P. Poulet
9 7.9842491755534198... *10^465 no 1992-04-15 F. W. Helenius
10 2.86879876441793479... *10^923 no 1997-05-13 R. M. Sorli
11 2.51850413483992918... *10^1906 no 2001-03-13 G. F. Woltman

Abundancy	First discovered MPN	Is it smallest?	Date	Discoverer
1	1	yes	ancient	-
2	6	yes	ancient	-
3	120	yes	ancient	-
4	30240	yes	~ 1638	R. Descartes
5	14182439040	yes	~ 1638	R. Descartes
6	34111227434420791224041472000	no	1643	P. Fermat
7	6.9545266398342727... *10^70	no	1902	A. J. C. Cunningham
8	2.34111439263306338... *10^161	no	1929	P. Poulet
9	7.9842491755534198... *10^465	no	1992-04-15	F. W. Helenius
10	2.86879876441793479... *10^923	no	1997-05-13	R. M. Sorli
11	2.51850413483992918... *10^1906	no	2001-03-13	G. F. Woltman

Various Records until January 2023

The factorizations of smallest -- for k >= 9 "only" smallest known -- k-perfect number for fixed abundancy are:

Abundancy 1:
1
Abundancy 2:
2 3
Abundancy 3:
2^3 3 5
Abundancy 4:
2^5 3^3 5 7
Abundancy 5:
2^7 3^4 5 7 11^2 17 19
Abundancy 6:
2^15 3^5 5^2 7^2 11 13 17 19 31 43 257
Abundancy 7:
2^32 3^11 5^4 7^5 11^2 13^2 17 19^3 23 31 37 43 61 71 73 89 181 2141 599479
Abundancy 8:
2^62 3^15 5^9 7^7 11^3 13^3 17^2 19 23 29 31^2 37 41 43 53 61^2 71^2 73 83 89 97^2 127 193 283 307 317 331 337 487 521^2 601 1201 1279 2557 3169 5113 92737 649657
Abundancy 9:
2^104 3^43 5^9 7^12 11^6 13^4 17 19^4 23^2 29 31^4 37^3 41^2 43^2 47^2 53 59 61 67 71^3 73 79^2 83 89 97 103^2 107 127 131^2 137^2 151^2 191 211 241 331 ...
Abundancy 10:
2^175 3^69 5^29 7^18 11^19 13^8 17^9 19^7 23^9 29^3 31^8 37^2 41^4 43^4 47^4 53^3 59 61^5 67^4 71^4 73^2 79 83 89 97 101^3 103^2 107^2 109 113 127^2 ...
Abundancy 11:
2^413.3^145 5^73 7^49 11^27 13^22 17^11 19^13 23^10 29^9 31^8 37^4 41^8 43^4 47^6 53 59 61^6 67^6 71^4 73^4 79^4 83^2 89^2 97^2 101^3 103^2 107^2 ...

Abund Smallest value Largest value Lowest 2-power Highest 2-power Largest eff. expo. Fewest factors * Most factors *
2 6 (0.5831981) 10^49724093.6 (18.5560326) 1 (0.5831981) 82589932 (18.5560326) 0 (0.5831981) 2 (0.5831981) 82589933 (18.5560326)
3 120 (1.5660066) 10^10.469 (3.2049844) 3 (1.5660066) 14 (3.2049844) 7 (3.2049844) 5 (1.5660066) 19 (3.2049844)
4 30240 (2.3337853) 10^45.204 (4.6452114) 2 (2.6806218) 37 (4.5312242) 17 (4.5312242) 8 (2.3415138) 57 (4.6365489)
5 10^10.148 (3.1516786) 10^100.276 (5.4419551) 7 (3.1516786) 61 (5.0442101) 45 (5.1777077) 17 (3.1516786) 103 (5.3046236)
6 10^20.189 (3.8391453) 10^192.162 (6.0923690) 15 (4.0050961) 92 (6.0923690) 79 (6.0362173) 31 (3.8391453) 164 (6.0923690)
7 10^56.150 (4.8620623) 10^312.074 (6.5772722) 29 (5.2987825) 177 (6.5408889) 108 (6.4271649) 71 (4.8620623) 307 (6.5528603)
8 10^132.917 (5.7237604) 10^613.291 (7.2528723) 47 (5.7578915) 253 (7.1699823) 156 (7.2528723) 137 (5.7237604) 466 (7.1485402)
9 10^286.749 (6.4926404) 10^1165.883 (7.8952666) 99 (6.6259527) 380 (7.8522986) 283 (7.7478296) 257 (6.4926404) 747 (7.8522986)
10 10^638.652 (7.2933919) 10^1877.645 (8.3718042) 175 (7.2933919) 534 (8.3718042) 434 (8.2500454) 492 (7.2933919) 1172 (8.3718042)
11 10^1738.495 (8.2948075) 10^1906.401 (8.3870050) 413 (8.2948075) 468 (8.3870050) 469 (8.3870050) 1088 (8.2948075) 1139 (8.3870050)

Italic printed values perhaps change in the future.
The identifiers for each MPN are given in parenthesis.
(*) The word factors means prime-factors.

Abund	Smallest value	Largest value	Lowest 2-power	Highest 2-power	Largest eff. expo.	Fewest factors *	Most factors *
2	6 (0.5831981)	10^49724093.6 (18.5560326)	1 (0.5831981)	82589932 (18.5560326)	0 (0.5831981)	2 (0.5831981)	82589933 (18.5560326)
3	120 (1.5660066)	10^10.469 (3.2049844)	3 (1.5660066)	14 (3.2049844)	7 (3.2049844)	5 (1.5660066)	19 (3.2049844)
4	30240 (2.3337853)	10^45.204 (4.6452114)	2 (2.6806218)	37 (4.5312242)	17 (4.5312242)	8 (2.3415138)	57 (4.6365489)
5	10^10.148 (3.1516786)	10^100.276 (5.4419551)	7 (3.1516786)	61 (5.0442101)	45 (5.1777077)	17 (3.1516786)	103 (5.3046236)
6	10^20.189 (3.8391453)	10^192.162 (6.0923690)	15 (4.0050961)	92 (6.0923690)	79 (6.0362173)	31 (3.8391453)	164 (6.0923690)
7	10^56.150 (4.8620623)	10^312.074 (6.5772722)	29 (5.2987825)	177 (6.5408889)	108 (6.4271649)	71 (4.8620623)	307 (6.5528603)
8	10^132.917 (5.7237604)	10^613.291 (7.2528723)	47 (5.7578915)	253 (7.1699823)	156 (7.2528723)	137 (5.7237604)	466 (7.1485402)
9	10^286.749 (6.4926404)	10^1165.883 (7.8952666)	99 (6.6259527)	380 (7.8522986)	283 (7.7478296)	257 (6.4926404)	747 (7.8522986)
10	10^638.652 (7.2933919)	10^1877.645 (8.3718042)	175 (7.2933919)	534 (8.3718042)	434 (8.2500454)	492 (7.2933919)	1172 (8.3718042)
11	10^1738.495 (8.2948075)	10^1906.401 (8.3870050)	413 (8.2948075)	468 (8.3870050)	469 (8.3870050)	1088 (8.2948075)	1139 (8.3870050)

Discovery dates of proper Multiply Perfect Numbers

Abund First MPN Smallest MPN Largest MPN Latest MPN
3 ancient (1.5660066) ancient (1.5660066) 1643 (3.2049844) 1643 (3.2049844)
4 1638 (2.3337853) 1638 (2.3337853) 1911 (4.6452114) 1929 (4.3351682)
5 1638 (3.1516786) 1638 (3.1516786) 1911 (5.4419551) 1990 (5.1744360)
6 1643 (4.1850902) 1907 (3.8391453) 1992 (6.0923690) 1993-05-?? (5.6720844)
7 1902 (5.0944883) 1911 (4.8620623) 1993 (6.5772722) 1994-01-09 (5.9403364)
8 1929 (5.9177287) 1990 (5.7237604) 1996-04-23 (7.2528723) 2022-05-22 (6.5244184)
9 1992-04-15 (6.9780083) 1995-12-06 (6.4926404) 2001-01-11 (7.8952666) 2022-06-05 (7.1993123)
10 1997-05-13 (7.6621574) 2013-01-03 (7.2933919) 2001-01-28 (8.3718042) 2022-06-11 (7.8125224)
11 2001-03-13 (8.3870050) 2022-09-07 (8.2948075) 2001-03-13 (8.3870050) 2022-09-07 (8.2948075)

Italic printed values perhaps change in the future.

Abund	First MPN	Smallest MPN	Largest MPN	Latest MPN
3	ancient (1.5660066)	ancient (1.5660066)	1643 (3.2049844)	1643 (3.2049844)
4	1638 (2.3337853)	1638 (2.3337853)	1911 (4.6452114)	1929 (4.3351682)
5	1638 (3.1516786)	1638 (3.1516786)	1911 (5.4419551)	1990 (5.1744360)
6	1643 (4.1850902)	1907 (3.8391453)	1992 (6.0923690)	1993-05-?? (5.6720844)
7	1902 (5.0944883)	1911 (4.8620623)	1993 (6.5772722)	1994-01-09 (5.9403364)
8	1929 (5.9177287)	1990 (5.7237604)	1996-04-23 (7.2528723)	2022-05-22 (6.5244184)
9	1992-04-15 (6.9780083)	1995-12-06 (6.4926404)	2001-01-11 (7.8952666)	2022-06-05 (7.1993123)
10	1997-05-13 (7.6621574)	2013-01-03 (7.2933919)	2001-01-28 (8.3718042)	2022-06-11 (7.8125224)
11	2001-03-13 (8.3870050)	2022-09-07 (8.2948075)	2001-03-13 (8.3870050)	2022-09-07 (8.2948075)

Old conjectures

The only odd multiply perfect number is 1. Consequently each (2-fold) perfect number is even (claimed already in the Middle Ages).
There are infinitely many perfect, i.e. 2-fold multiply perfect, numbers.
For each fixed abundancy > 2, there are only finitely many multiply perfect numbers.
For each fixed prime power, there is at least one MPN which has exactly this prime power in its prime factorization (lowest two-power-exponents for to-be-discovered-MPNs are 331, 336, 347, ... and lowest three-power exponents are 127,134, ... ).

Distribution of the 5311 (until 2013-12-31) known Multiply Perfect Numbers

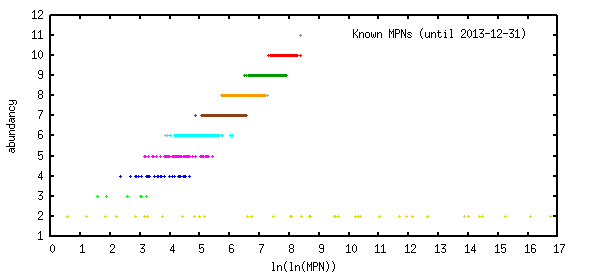
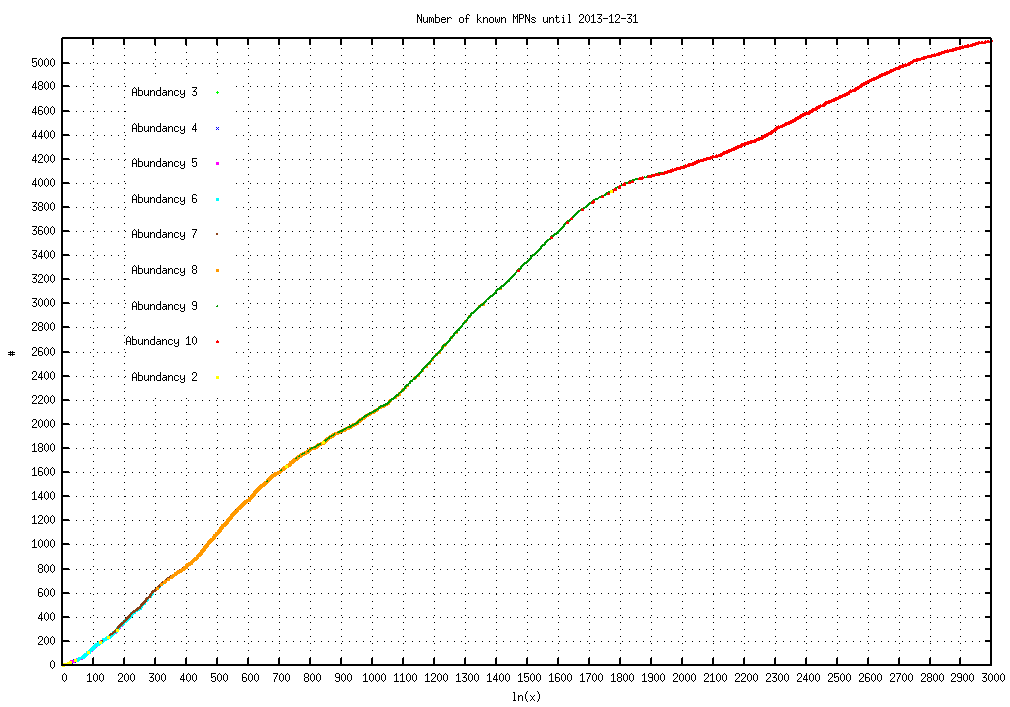
MPN-dist-diagram
If the number of MPNs up to a given limit x is proportional to ln(x), then the density of the MPNs should be proportional to 1/x. And a further picture to visualize the density of the known MPNs. In first approximation it may be a Poisson-distribution. You guess that surely there are missing MPNs at last at the currently known 4000th MPN, but also highly probable earlier. Finally a best linear fit for the smallest 3600 known MPNs except the first 100 MPNs to avoid 'start-effects' was done on a logarithmic scale. For these 3500 numbers this least-quadratic error approximation results a correlation coefficient of 0.99815 with # MPN ~ 2.2328ln(x)-48.3655.
Richard Schroeppel stated that he constructed all MPNs < 10⁷⁰ in the eighties of the twenty-century (but probably only 1990), i.e. he proved that there exist exactly 258 MPNs smaller than 10⁷⁰ -- and besides showed that there are no odd MPNs < 10⁹⁰ except 1. In March 2008 Achim Flammenkamp finally constructed all MPNs < e³⁵⁰ by an exhaustive tree-search, i.e. proved that there are no further but the 730 known MPNs. Here is a small paper presenting the theoretical and practical background to this computation.

The Two-Power exponent of a MPN

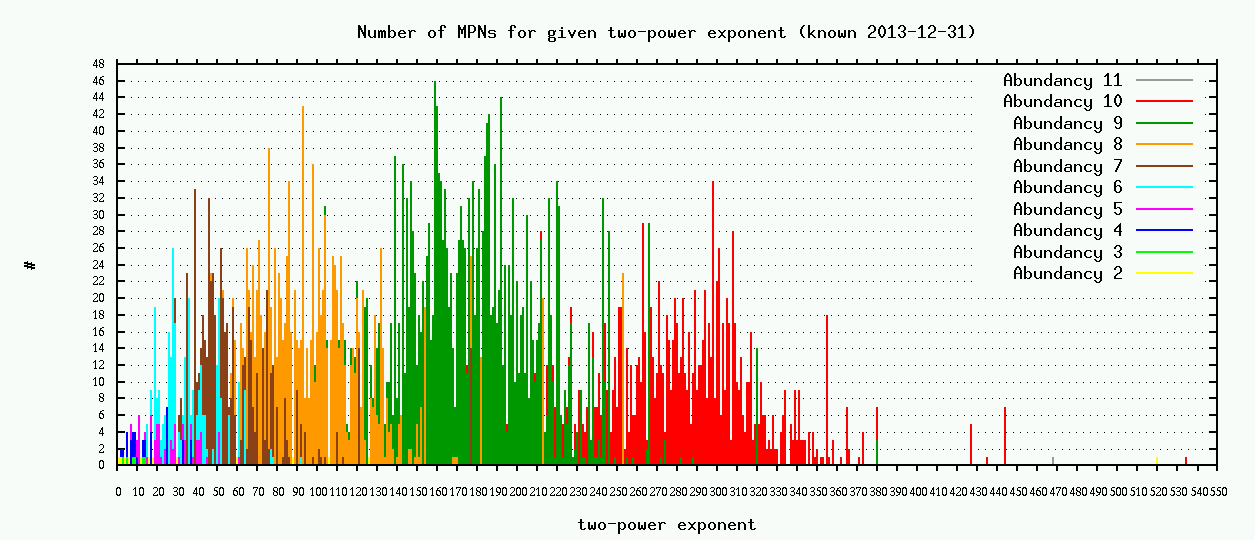
And here is a false color diagram for the distribution of these MPNs

Let us introduce Fred Helenius' notion of the effective exponent. The prime p=2 is special compared to other primes, because p-1 has only the trivial divisor 1. A consequence of this fact is, only if p equals 2, then numbers of the form pⁿ-1 could be prime. Assume a fixed MPN m has in its prime factorization the two-power exponent k. This means that σ(m) has a factor 2^k+1-1. Depending on k this factor may have some prime divisors of the form 2ⁿ-1. Because we are considering a MPN, σ(2ⁿ-1) = 2ⁿ must be also a factor of this MPN itself, if 2ⁿ-1 occurs exactly onetime! Hence the original prime-power 2^k may produce immediately further two-powers. Or put it in other words: only the `remainder' of this exponent k must be produced by other prime-powers. So, the exponent is effectively reduced in consideration to the to-be-generated two-power factors by other prime-powers. Primes of the form 2ⁿ-1 are called Mersenne Primes and are known up to high values of n. Thus we have to check which Mersenne Prime 2ⁿ-1 divide a given 2^k+1-1 exactly onetimes. Subtracting k+1 by such Mersenne Prime exponents n gives the effective exponent of k. There is a small blemish in this model: small primes of the form q=2ⁿ-1 may as well be produced by other prime-powers (than two-powers) of a MPN, such that the exponent of q is not 1 in the factorization of the MPN, but larger. Hence we have probably overestimated the correction of the two-power exponent a bit.
The two-power exponent k of a (2-fold) perfect number has always an effective exponent of 0. For such an effective exponent of 0, there seems to exist only the corresponding (2-fold) MPN except in the case k equals 2. If k = in-1 with n the exponent of a Mersenne Prime and i a small number, the effective exponent is at most n(i-1), roughly 1-1/i of the given exponent k. Such exponents k are typically the largest two-power exponents for which a MPN for a fixed proper abundancy exists: 61=2*31-1, 92=3*31-1, 177=2*89-1, 253=2*127-1, 320=3*107-1,380=3*127-1.
Finally, for a given two-power exponent k the effort to compute a MPN with an even factor of 2^k seems more related to its effective exponent than to k --- this is heuristically convincing and seems likely to be the reason this quantity was invented --- and lastly the distribution of the prime-exponents of a `typical' MPN seems proportional to the effective exponent than to the two-power exponent.

References collected by Rich Schroeppel

R. D. Carmichael & T. E. Mason, Notes on Multiply Perfect Numbers, Including a Table of 204 New Ones and the 47 Others Previously Published, Proc. Indiana Academy of Science, 1911 p257-270.
Leonard Eugene Dickson, History of the Theory of Numbers, 1919, v.1 p33-38.
Paul Poulet, La Chasse Aux Nombres, Fascicule I, Bruxelles, 1929, p9-27.
Benito Franqui & Mariano Garcia, Some New Multiply Perfect Numbers, American Math Monthly 1953 p459-462.
Alan L. Brown, Multiperfect Numbers, Scripta Mathematica 1954 p103-106.
Benito Franqui & Mariano Garcia, 57 New Multiply Perfect Numbers, Scripta Mathematica 1954 p169-171.
Alan L. Brown, Multiperfect Numbers - Cousins of the Perfect Numbers - No. 1, Recreational Mathematics Magazine #14, Jan/Feb 1964.
Motoji Yoshitake, Abundant Numbers, Sum of Whose Divisors are an Integer Times the Number, Sugaku Seminar, v.18 n.3 p50-55, 1979.
private communications from M. Garcia, Stephen Gretton, M. Yoshitake, Fred Helenius, and Achim Flammenkamp.

Further Infos

Fred Helenius's Multiperfect numbers
Ron Sorli's Thesis: Algorithms in the Study of Multiperfect and Odd Perfect Numbers 2003, Sydney, Australia and its first 9 pages .
A gziped-tar archive containing the sigma-chain database and its C-sourcecode library (486kB) to access and maintain it (version 4.1d).
Eric Weisstein's explanations of MPNs. .
The haunt for improper Multiperfect Numbers :)

Please sent any comments or questions concerning this web page to:

Achim Flammenkamp
2023-01-21 15:26 UTC+1