Game of Life

Introduction

Game of Life is a cellular automaton on an infinite quadratic grid. Each grid cell is either alive/on or dead/off. The new state of each cell is computed in discrete timesteps and is determinated by it's old state and the sum of the alive cells among its surrounding 8 nearest neighbours cells. All these changes are simultaneously over the whole, infinite grid!
The Game of Life rules let a cell in the next generation only alive if a living cell is either surrounded by either 2 or 3 alive cells, the survive condition, or a dead cell flips into the alive state in the next generation if it is surrounded by exactly 3 living cells, the borne condition. Otherwise it dies or stays dead. Therefore a given initial pattern, a collection of alive cells in a universe of dead cells, develops according to these rules over the generations and produces various configurations.
These special rules were invented 1970 by the mathematician J.H. Conway to garanty that the cellular automaton is on the boundary between unbounded growth and decay into dullness. It was proven that it's chaotic behaviour is unpredictable and it could be used to build an universal turing-machine and even an universal constructor. One of the important open problems is whether a sufficient large random populated universe will develop selforganization structures.

A 143-bit Garden Of Eden object 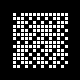, constructed January 1991. Can you find a smaller one --- i.e. proving that your example has no predecessor in Game of Life and has fewer living cells? YES

Collected Resources

There is nothing as interesting as Life !

Back to my HomePage

Achim Flammenkamp
Last update: Bielefeld, den 2011-12-19 17:22:07   o'clock