Fields of investigation of L.D. Pustyl'nikov
in mathematics and in its applications
- I. Qualitative theory of ordinary differential equations and dynamical systems
- 1) Reducibility to analytic normal form of nonautonomous transformations and differential equations in the neighbourhod of an equilibrium point ([2], [5], [53], [70])
- 2) The study of stability of nonautonomous conservative (and closed to them) systems in the neighbourhood of a fixed point and of an arbitrary trajectory ([3], [6], [15], [53])
- 3) The construction of periodic, quasiperiodic solutions, and the investigation of stability in finite and infinite-dimensional hamiltonian systems ([4], [6], [9], [15], [20], [22], [25], [28], [54], [55], [58], [65], [117])
- 4) Construction of strange attractors and bifurcations in infinite-dimensional systems of ordinary differential equations ([41], [102])
- 5) Construction of explicit and asymptotic solutions in conservative systems ([22], [40])
- 6) A control and an identification in systems of ordinary differential equations ([12], [149)
- II. Final motions in mechanics of systems and particles
- 1) The study of an acceleration mechanism in models associated with Fermi-Ulam model ([1], [4], [6], [16], [27], [30], [33], [47], [53], [56], [110], [112], [116], [124])
- 2) Construction of oscillatory motions ([1], [4], [6], [20], [28], [34], [71], [117])
- 3) Final motions in n-body problem of celestial mechanics ([34], [71])
- III. Application of dynamical systems to rigorous justification of laws in statistical mechanics, accelerators theory and plasma physics
- 1) Rigorous justification of the second law of thermodynamics in Poincarè models for nonequilibrium gas ([35], [53], [74])
- 2) Construction of phase transitions in Frenkel-Kontorovou model (829], [51])
- 3. Qualitative behaviour of trajectories of systems with
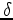 -type interaction, arising in the accelerators theory and plasma physics ([9], [15], [20], [28], [33], [117])
-type interaction, arising in the accelerators theory and plasma physics ([9], [15], [20], [28], [33], [117])
- 4) Quantum chaos ([75], [96], [109], [114])
- IV. Some problems of analysis and number theory
- 1) Application of ergodic theory to finding strong estimates of Weyl sums and to the remainder term in the law of the distribution of the fractional parts of polynomials ([13], [39], [46], [48], [49], [50], [72], [106])
- 2) Probability and ergodic laws in the distribution of fractional parts of polynomials ([75], [85], [114])
- 3) Problems of distribution of quadratic residues and non-residues ([45], [64], [95], [104], [106])
- 4) New theory of generalized continued fractions (849], [50], [64], [72], [103], [104], [106], [109])
- 5) Classical zeta-function and Riemann hypothesis ([36], [73], [81], [84], [107], [120])
- V. Probability theory ([82], [85], [101], [105])
- VI. Toeplitz and Hankel matrices and their applications
- 1) The structure of Toeplitz and Hankel matrices ([10], [18], [31])
- 2) Fast computations in problems of linear algebra connected with Toeplitz and Hankel matrices ([11], 818], [31])
- 3) Fast prediction of random processes ([18], [31])
- 4) Toeplitz and Hankel integral operators ([18])
- VII. Combinatorics ([94], [123])
- VIII. Geometry ([111], [118], [119])
- IX. Ergodic theory in partial differential equations ([83])
- X. Theory of singularities ([89], [92], [98])
- XI. Applications of mathematics to some fields of discrete optimization and energetics ([7], [8], [14], [17], [19], [21], [23], [24], [26], [32], [37], [38], [42], [43], [44])



Next: About this document ...
Olga Pustylnikov
2008-02-17
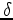 -type interaction, arising in the accelerators theory and plasma physics ([9], [15], [20], [28], [33], [117])
-type interaction, arising in the accelerators theory and plasma physics ([9], [15], [20], [28], [33], [117])