Official Nuclid Data
Other data sources
Quality of nuclide data/discovery
- dubious, contradictive data [118-293]
- only Z and A of the nuclid published [Rf-264] list of only known-to-exist nuclides
- 2) and (one) mode of decay given [Hs-263] list of shallow known nuclides
- 3) and (estimation of) T1/2 given [Lr-262]
- 4) and spin given [Fm-255]
- 5) and mass given [Sg-265]
To verify a claim of production of a certain nuclide, it should be at least a
member of item 3, but firstly class 4 give a true chance of refutability.
A list of known nuclides.
Distribution of "stable" nuclides
- There are 277 nuclides with Z <= 83 and which are stable to simple beta-decay.
- Of these 277 nuclides, 68 may decay by double-beta-decay.
- Also, of these 277 nuclides 84 may decay by alpha-decay.
- Therefore 147 nuclides are stable to any kind of alpha or beta decay.
- One of these 147, namely He-5, decays by n-emittion in about 10-21 sec.
- and 54 are instable to cluster-decay (C-12, O-16, Ne-20, e.t.c.).
- But, as of March 2002, there are 237 nuclides for which a decay (still) has not been observed.
- There are 275 nuclides which have half life > 1012 years, none of these has Z > 83.
- Only 6 of these 275 nuclides are beta-instable (In-115, Te-123, Cd-113, V-50, Ca-48, Zr-96),
but Ca-48 and Zr-96 decay by double beta-decay.
- There are 9 further nuclides having a half life > 109 years,
namely Pt-190, Sm-147, La-138, Rb-87, Re-187, Lu-176, Th-232, U-238, K-40.
- There are no stable isobares of A= 5, 8, 147, 149, 182, 183, 184, 186 and >= 210.
Moreover there are no stable isotopes for Z=43, 61, 74(Wolfram) and >= 84 ---
further to discover.
| T1/2 | # | Count Trend |
| unobservable | 237 | decreasing |
| > 1015 years | 269 | fixed? |
| > 1012 years | 275 | fixed |
| > 109 years | 284 | fixed |
| > 106 years | 305 | probably fixed |
| > 1000 years | 335 | speculative |
| > 1 year | 395 | increasing? |
| > 1 day | 623 | increasing |
| > 1 hour | 864 | increasing |
| > 10 min | 1084 | increasing |
| > 1 min | 1442 | increasing |
| > 10 sec | 1723 | increasing |
| > 1 sec | 2087 | increasing |
| unknown | 70 | fluctuating |
| > 10-9 secs | 2976 | increasing |
| > 10-12 secs | 2977 | increasing |
| > 10-18 secs | 2978 | increasing |
| > 10-24 secs | 3001 | increasing |
These occur in 114 different elements (excluding Z=0).
Observed Modi of Decay
The parent nuclide is named X and consist of a nucleons including z protons.
The child nuclide is called Y and electrons will be denoted by e
- alpha-decay
- emittion of an He-4 nuclid: azX --> a-4z-2Y2- + 42He2+
- beta-decay
- the number of nucleons stay constant. Transformation from neutrons into protons or reverse.
- beta- -decay
- azX --> az+1Y+ + e-
An electron will be emitted.
- beta+ -decay
- azX --> az-1Y- + e+
A positron will be emitted.
- Electron capture
- azX --> az-1Y
An inner electron of the atom will be captured by its parent nucleus and transform so a proton-electron pair into a neutron.
- double-beta-decay
- either
azX --> az+2Y2+ + 2e-
or
azX --> az-2Y2- + 2e+
- p emission
-
azX --> a-1z-1Y- + p
- n emission
-
azX --> a-1zY + n
- cluster decay
- emittion of a nuclide heavier than 42He, but far
lighter than the parent nuclide. These cluster nuclides are strong bound nuclides. Typical examples are 146C, 208O.
Maybe considered as a generalization of the alpha-decay.
- spontanious fission
- Breaking of the nuclide into two parts and some single neutrons. The exact
values of p and z of the two child nuclides will variate.
- gamma decay
- The nucleons stay the same. Also denoted as internal transition. A
so-called isomere will emitte a photon going into a lower internal nuclide state.
Sadly, this (classical) "binding energy" does not reflect the internal
strength of nucleon binding in a nuclide.
It is a purely mathematical definition with tiny practicable information value.
This is mainly due to historical reasons --- physicists are also humans
who don't like to change their old habits. But to stay factual:
"binding energy" of a atom of mass M consisting of Z protons (and Z electrons)
and N neutrons is defined as
Z(mp+me) + N mn - M.
For the physicaly irrelevance look only at the beta- decay of 3H into
3He. Tritium (H-3) has a higher binding energy than He-3 but it
decays exotherm! Ridiculous. Or 62Ni has a higher "binding energy" than
56Fe, which is the strongest bound nuclide at all, and the correct
statement is of important astrophysical relevance.
The error comes from the assumption that in a nucleous are distinguishable particles called neutrons and protons, but this is false. There is quantum-mechanically only one kind of particle which maybe interpreted like a superposition
of proton and neutron --- not to question whether this is really a particle. :)
Another (more intuitive) interpretation is the continous exchange of pions
between the nucleons which blurs the difference between proton and neutron.
Thus the correct formula to measure the binding energy must be of the form:
(Z+N)mnucleon - M.
But what is "the" nucleon --- respectively its mass?
It doesn't matter much, you may select mp or mn
or any value between these two.
This only shifts the zero level of your binding energy.
You could even accept the mass defect,
defined to be M - (Z+N)mC-12/12,
as a kind of (inverse) binding energy, if you like the zero level to be obtained
by the Carbon-12 isotope.
I personally prefer to choose mn, because then all nuclides get
positive binding energy.
Have a look at the first atoms and the strongest bound atoms:
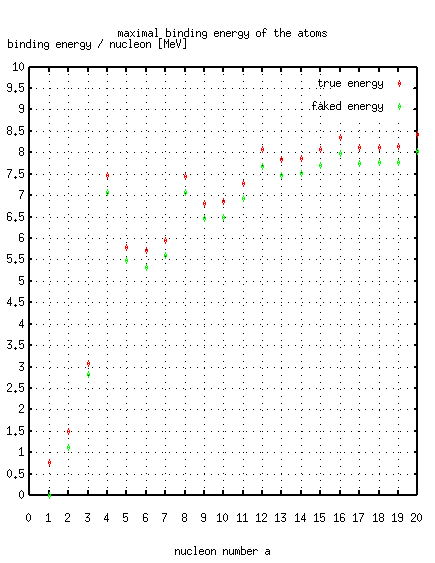
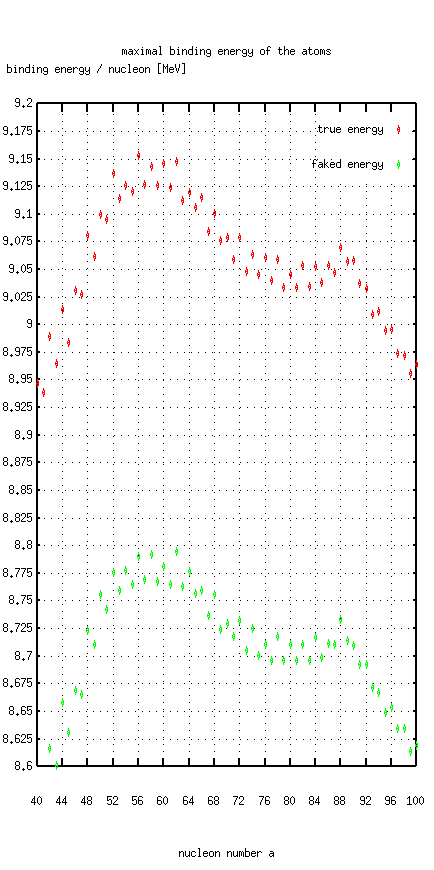 .
.
Achim Flammenkamp
last updated:

 .
.