Finite Topologic Spaces and finite Preorders / Posets

There is an intrigued similarity between the number of finite topologic spaces and the length of shortest addition chains. Thus let us first explain what a finite topologic space is.
You start with a finite set B of cardinality k. Next you consider its power set P(B) which is by definition the set of all the 2^k-many possible subsets of B. Then a finite topologic space S is any subset of such a powerset which satisfies the following two conditions: It must contain the empty set and the set B and secondly for any two elements of S it must be closed under intersection and union.
You may translate this definition of finite topologies into binary 0-1-strings of length k. Then the intersection becomes the binary and-operation and the union the binary or-operation on the strings. Lastly, denote the number of elements of S, which are called open sets, by n.
Then one may ask: At least how many elements k must a set contain such that a finite topologic space on it can exist which consists of exactly n open sets?
This unique sequence of numbers (m(n))_n starts as 0,1,2,2,3,3,4,3,4,... like the sequence of the length of shortest addition chains (ℓ(n))_n. As a matter of fact for all n ≤ 128 with n ≠ 71 holds ℓ(n)=m(n) but 9 = ℓ(71) > m(71) = 8.
Because there is a on-to-one mapping of finite topologic spaces to preorders of finite sets, we also can consider preorders. Define for any x, y ∈ B a natural preorder on a topologic space as x ≤ y if the closure of x is a subset of the closure of y. The closure of any element x ∈ B is defined as the intersection of all open sets of the topologic space which contain x.
Notice, because we are interested only in the minimal number of points of a topologic space, we can restrict to non-isomorphic T₀-topologies, i.e. all points must be topologically distinguishable. And then finite preorders become finite posets, i.e. finite partial order sets. The upper sets (upwards closed sets) of a poset, correspond one-to-one to the open sets of the associated T₀-topology. Any poset may be represented by a directed graph where the vertices correspond to the points/elements and its directed edges correspond to the order-relations. If this graph is drawn on a piece of paper such that the parents of points are always above their children, then we can omit the directions of the edges in this picture. As an example the minimal poset with ℓ(n) ≠ m(n) is presented next:

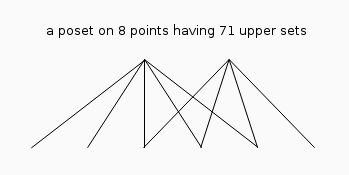
If you delete both top points the 6 remaining points have no relations and generate 2⁶ upper sets. Adding then only the left point give rise to (2⁵+1)2¹ upper sets, on the other hand adding then only the right point give rise to 2²(2⁴+1) upper sets. Finally adding the last removed point left adds 2²+1 respectively on the right adds 2¹+1 further open sets. This poset and its dual poset (where all order-relations are inverted) are the only posets on 8 points having 71 upper sets.

K. Ragnarsson and B. E. Tenner reported in their paper OBTAINABLE SIZES OF TOPOLOGIES ON FINITE SETS from 2008, that M. Erné and K. Stege in their report entitled "Counting finite posets and topologies", Tech. Report 236 , University of Hannover, 1990, already had computed the values T(k,n) for k ≤ 11 and all n, which enabled them to answer my question for n ≤ 379. I recomputed these numbers m(n) for n ≤ 379 and can now state that they equal ℓ(n) with the exception of 12 values, namely n ∈ {71, 139, 141, 142, 263, 267, 269, 275, 277, 278, 282, 284} for which ℓ(n)=m(n)+1 -- i.e. the minimal number of points m(n) needed for a topology of n open sets is 1 less than the length of a shortest addition chain for those numbers n.
It is tempting to conjecture that m(n) is a lower bound for ℓ(n). Sadly computing m(n) seems to be much harder than to compute ℓ(n). Thus it seems more useful to conjecture ℓ(n) as an upper bound for m(n).

Finally here is a table of m(n) with n ≤ 480 and a list of relations between finite topologic spaces resp. finite posets and addition chains to get those m(n) with 379 ≤ n ≤ 478 from the T(k,n) values for k ≤ 11.
Last Sunday in October 2016, I was able to compute all T(k,n) values for k ≤ 14 and thus could extend the m(n)-sequence up to its 2790th term.
Until 21th November 2016, I was able to compute all T(15,n) values, too, and therefore could extend this m(n)-sequence up to its 4966th term.

Footnote: T(k,n) denotes the number of non-isomorphic T₀-topologic spaces made up by k elements and having n open sets.